Совет 1: Как обнаружить периметр шестиугольника

Как знаменито, периметром плоской фигуры именуется длина ограничивающей ее линии. Дабы обнаружить периметр многоугольника довольно сложить длины его сторон. Для этого придется измерить длины всех составляющих его отрезков. Если же многоугольник положительный, то задача нахождения периметра гораздо упрощается.



Вам понадобится

• – линейка;
• – циркуль.

Инструкция

1. Дабы обнаружить периметр шестиугольника , измерьте и сложите длины всех его шести сторон. Р = а1+а2+а3+а4+а5+а6,где P – периметр шестиугольника , а а1, а2 … а6 – длины его сторон.Единицы измерения всей из сторон приведите к одному виду – в этом случае довольно будет сложить только числовые значения длин сторон. Единица измерения периметра шестиугольника будет совпадать с единицей измерения сторон.

2. Пример.Имеется шестиугольник с длинами сторон 1 см, 2 мм, 3 мм, 4 мм, 5 мм, 6 мм. Требуется обнаружить его периметр.Решение.1. Единица измерения первой стороны (см) отличается от единиц измерения длин остальных сторон (мм). Следственно, переведите: 1 см = 10 мм.2. 10+2+3+4+5+6=30 (мм).

3. Если шестиугольник положительный, то дабы обнаружить его периметр, умножьте длину его стороны на шесть:Р = а * 6,где а – длина стороны верного шестиугольника .Пример.Обнаружить периметр верного шестиугольника с длиной стороны равной 10 см.Решение: 10 * 6 = 60 (см).

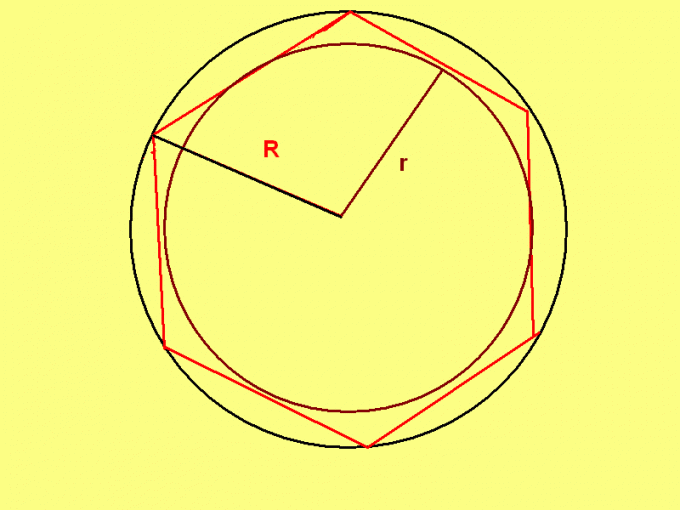
4. Положительный шестиугольник владеет уникальным свойством: радиус описанной вокруг такого шестиугольника окружности равен длине его стороны. Следственно, если знаменит радиус описанной окружности, до воспользуйтесь формулой:P = R * 6,где R – радиус описанной окружности.

5. Пример.Рассчитать периметр положительного шестиугольника , писанного в окружность диаметром 20 см.Решение. Радиус описанной окружности будет равен: 20/2=10 (см).Следственно, периметр шестиугольника : 10 * 6 = 60 (см).

6. Если по условиям задачи задан радиус вписанной окружности, то примените формулу:P = 4 * ?3 * r,где r – радиус вписанной в верный шестиугольник окружности.

7. Если вестима площадь положительного шестиугольника , то для расчета периметра используйте следующее соотношение:S = 3/2 * ?3 * а?,где S – площадь верного шестиугольника . Отсель дозволено обнаружить а = ?(2/3 * S / ?3), следственно:Р = 6 * а = 6 * ?(2/3 * S / ?3) = ?(24 * S / ?3) = ?(8 * ?3 * S) = 2?(2S?3).

Совет 2: Как обнаружить площадь шестиугольника

По определению из планиметрии верным многоугольником именуется рельефный многоугольник, у которого стороны равны между собой и углы так же равны между собой. Положительный шестиугольник является верным многоугольником, с числом сторон равным шести. Существует несколько формул для расчета площади положительного многоугольника.

Инструкция

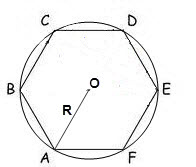
1. Если знаменит радиус окружности описанной около многоугольника, то его площадь дозволено вычислить по формуле:S = (n/2)•R?•sin(2?/n), где n – число сторон многоугольника, R – радиус описанной окружности, ? = 180?.В верном шестиугольнике все углы равны 120°, следственно формула будет иметь вид:S = ?3 * 3/2 * R?



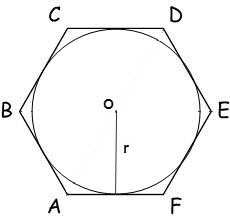
2. В случае, когда окружность с радиусом r вписана в многоугольник, его площадь вычисляется по формуле:S = n * r? * tg(?/n), где n – число сторон многоугольника, r – радиус вписанной окружности, ? = 180?.Для шестиугольника эта формула принимает вид:S = 2 * ?3 * r?



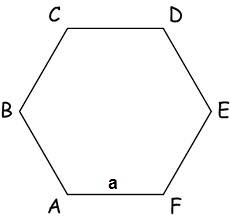
3. Площадь верного многоугольника так же дозволено вычислить, зная лишь длину его стороны по формуле:S = n/4 * a? * ctg(?/n), n – число сторон многоугольника, a – длина стороны многоугольника, ? = 180?.Соответственно площадь шестиугольника равна:S = ?3 * 3/2 * a?

Совет 3: Как обнаружить периметр фигуры

В задачах по геометрии зачастую требуется обнаружить периметр фигуры . Периметром фигуры именуется длина ограничивающей ее линии. Дозволено, безусловно, легко измерить длину этой линии. Впрочем, итоги таких измерений могут оказаться неудовлетворительно точными. Помимо того, измерение длины косой линии – достаточно-таки сложный процесс. Следственно на практике и при решении геометрических задач обыкновенно применяют особые формулы.



Вам понадобится

• линейка, циркуль, калькулятор

Инструкция

1. Дабы обнаружить периметр фигуры , ограниченной ломаной линией, сложите длины всех составляющих ее отрезков. Если длины отрезков неведомы, измерьте их с подмогой циркуля и линейки. Если фигура имеет относительно крупные размеры, воспользуйтесь рулеткой. Единицей измерения периметр а будут служить те же единицы, в которых заданы (измерялись) длины составляющих отрезков. Если единицы измерения различные, то их нужно привести к одному виду.Скажем, если земельный участок имеет треугольную форму с длинами сторон 10, 20 и 30 метров, соответственно, то его периметр составит: 10 + 20 + 30 (м).

2. Для нахождения периметр а примитивных геометрических фигур, воспользуйтесь особыми формулами.Дабы обнаружить периметр ромба (в частности, квадрата), умножьте длину его стороны на четыре. То есть, воспользуйтесь следующими формулами:П(ромб) = П(квадрат) = 4 * с,где с – длина стороны ромба (квадрата), П – его периметр .

3. Для нахождения периметр а параллелограмма (в частности, прямоугольника), сложите его длину и ширину и умножьте на два (под длиной и шириной подразумеваются длины 2-х смежных сторон). Нагляднее, это дозволено записать в дальнейшем виде:П(параллелограмм) = П(прямоугольник) = 2 * (д + ш), где:д и ш – длина и ширина параллелограмма (прямоугольника), соответственно.

4. Дабы обнаружить периметр круга, вычислите длину ограничивающей его окружности. Для этого воспользуйтесь классической формулой:П(круг) = ? * Д илиП(круг) = 2 * ? * Р,где: Д – диаметр круга, Р – радиус круга, ? – число «пи», приблизительно равное 3,14.

5. Если знаменита длина диагонали квадрата, то для нахождения его периметр а используйте следующую формулу:П(квадрат) = 2?2 * д,где д – длина диагонали квадрата.

6. Периметр квадрата дозволено рассчитать, применяя информацию о его площади. Для этого воспользуйтесь дальнейшим правилом:П(квадрат) = 4 * ?Sкв,где Sкв – площадь квадрата.

Совет 4: Как обнаружить периметр верного многоугольника

Периметром многоугольника называют замкнутую ломаную линию, составленную из всех его сторон. Нахождение длины этого параметра сводится к суммированию длин сторон. Если все отрезки, образующие периметр такой двухмерной геометрической фигуры, имеют идентичные размеры, многоугольник именуется положительным. В этом случае вычисление периметра гораздо упрощается.

Инструкция

1. В самом простом случае, когда знамениты длина стороны (а) верного многоугольника и число вершин (n) в нем, для вычисления длины периметра (Р) легко перемножьте эти две величины: Р = а*n. Скажем, длина периметра верного шестиугольника со стороной в 15 см должна быть равна 15*6=90 см.

2. Вычислить периметр такого многоугольника по знаменитому радиусу (R) описанной около него окружности тоже допустимо. Для этого придется вначале выразить длину стороны с применением радиуса и числа вершин (n), а после этого умножить полученную величину на число сторон. Дабы рассчитать длину стороны умножьте радиус на синус числа Пи, поделенного на число вершин, а итог удвойте: R*sin(?/n)*2. Если вам комфортнее вычислять тригонометрическую функцию в градусах, замените число Пи на 180°: R*sin(180°/n)*2. Периметр вычислите умножением полученной величины на число вершин: Р = R*sin(?/n)*2*n = R*sin(180°/n)*2*n. Скажем, если шестиугольник вписан в круг с радиусом 50 см, его периметр будет иметь длину 50*sin(180°/6)*2*6 = 50*0,5*12 = 300 см.

3. Схожим методом дозволено посчитать периметр, не зная длины стороны положительного многоугольника , если он описан около окружности с вестимым радиусом (r). В этом случае формула для вычисления размера стороны фигуры будет отличаться от предыдущей лишь задействованной тригонометрической функцией. Замените в формуле синус на тангенс, дабы получить такое выражение: r*tg(?/n)*2. Либо для расчетов в градусах: r*tg(180°/n)*2. Для вычисления периметра увеличьте полученную величину в число раз, равное числу вершин многоугольника : Р = r*tg(?/n)*2*n = r*tg(180°/n)*2*n. Скажем, периметр восьмиугольника, описанного вблизи круга с радиусом в 40 см, будет примерно равен 40*tg(180°/8)*2*8 ? 40*0,414*16 = 264,96 см.