Совет 1: Как обнаружить высоту в трапеции, если знамениты все стороны
Трапецией именуется рельефный четырёхугольник, у которого параллельны две противоположные стороны и непараллельны две другие. Если все противоположные стороны четырёхугольника попарно параллельны, то это параллелограмм.

Вам понадобится
- – все стороны трапеции (AB, BC, CD, DA).
Инструкция
1. Непараллельные стороны трапеции именуются боковыми сторонами, а параллельные – основаниями. Линия между основаниями, перпендикулярная к ним – высота трапеции . Если боковые стороны трапеции равны, то она именуется равнобедренной. Вначале разглядим решение для трапеции , которая не является равнобедренной.
2. Проведите отрезок BE из точки B к нижнему основанию AD параллельно боковой стороне трапеции CD. От того что BE и CD параллельны и проведены между параллельными основаниями трапеции BC и DA, то BCDE – параллелограмм, и его противоположные стороны BE и CD равны. BE=CD.
3. Разглядите треугольник ABE. Вычислите сторону AE. AE=AD-ED. Основания трапеции BC и AD вестимы, а в параллелограмме BCDE противолежащие стороны ED и BC равны. ED=BC, значит, AE=AD-BC.
4. Сейчас узнайте площадь треугольника ABE по формуле Герона, вычислив полупериметр. S=корень(p*(p-AB)*(p-BE)*(p-AE)). В этой формуле p – полупериметр треугольника ABE. p=1/2*(AB+BE+AE). Для вычисления площади вам знамениты все нужные данные: AB, BE=CD, AE=AD-BC.
5. Дальше запишите площадь треугольника ABE иным методом – она равна половине произведения высоты треугольника BH и стороны AE, к которой она проведена. S=1/2*BH*AE.
6. Выразите из этой формулы высоту треугольника, которая является и высотой трапеции . BH=2*S/AE. Вычислите её.
7. Если трапеция равнобедренная, решение дозволено исполнить по-иному. Разглядите треугольник ABH. Он прямоугольный, потому что один из углов, BHA, прямой.
8. Проведите из вершины C высоту CF.
9. Изучите фигуру HBCF. HBCF прямоугольник, от того что две его стороны – высоты, а другие две являются основаниями трапеции , то есть углы прямые, а противолежащие стороны параллельны. Это значит, что BC=HF.
10. Посмотрите на прямоугольные треугольники ABH и FCD. Углы при высотах BHA и CFD прямые, а углы при боковых стороны х BAH и CDF равны, потому что трапеция ABCD равнобедренная, значит, треугольники подобны. Потому что высоты BH и CF равны либо боковые стороны равнобедренной трапеции AB и CD равны, то и сходственные треугольники равны. Значит, их стороны AH и FD тоже равны.
11. Обнаружьте AH. AH+FD=AD-HF. Потому что из параллелограмма HF=BC, а из треугольников AH=FD, то AH=(AD-BC)*1/2.
12. Дальше из прямоугольного треугольника ABH по теореме Пифагора рассчитайте высоту BH. Квадрат гипотенузы AB равен сумме квадратов катетов AH и BH. BH=корень(AB*AB-AH*AH).
Совет 2: Как обнаружить площадь трапеции
Трапеция – геометрическая фигура, представляющая собой четырехугольник, у которого две стороны, которые именуются основаниями, параллельны, а две другие – не параллельны. Их называют боковыми сторонами трапеции . Проведенный через середины боковых сторон отрезок именуется средней линией трапеции . Трапеция может иметь различные длины боковых сторон либо идентичные, в этом случае она именуется равнобокой. Если одна из сторон – перпендикулярна к основанию, то трапеция будет прямоугольной. Но куда практичнее знать, как обнаружить площадь трапеции .
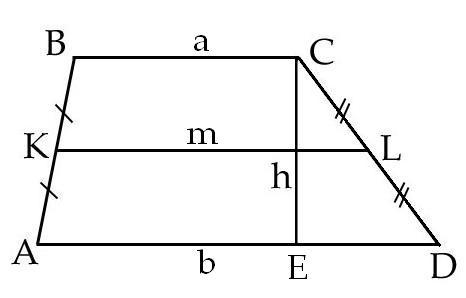
Вам понадобится
- Линейка с миллиметровыми делениями
Инструкция
1. Измерьте все стороны трапеции : AB, BC, CD и DA. Запишите итоги своих измерений.
2. На отрезке AB подметьте середину – точку K. На отрезке DA подметьте точку L, которая тоже находится на середине отрезка AD. Объедините точки K и L, полученный отрезок KL будет являться средней линией трапеции ABCD. Измерьте отрезок KL.
3. Из вершины трапеции – тоски С опустите перпендикуляр на ее основание AD о отрезок СЕ. Он будет являться высотой трапеции ABCD. Измерьте отрезок СЕ.
4. Назовем отрезок KL буквой m, а отрезок СЕ – буквой h, тогда площадь S трапеции ABCD вычислите по формуле: S=m*h, где m – средняя линия трапеции ABCD , h – высота трапеции ABCD.
5. Есть еще одна формула, дозволяющая рассчитать площадь трапеции ABCD. Нижнее основание трапеции – AD назовем буквой b, а верхнее основание BC – буквой а. Площадь определим по формуле S=1/2*(a+b)*h, где a и b – основания трапеции , h – высота трапеции .
Видео по теме
Совет 3: Как обнаружить высоту трапеции, если вестима площадь
Под трапецией подразумевается четырехугольник, у которого две из четырех его сторон параллельны между собой. Параллельные стороны являются основаниями данной трапеции , две другие же являются боковыми сторонами данной трапеции . Обнаружить высоту трапеции , если вестима ее площадь, будет дюже легко.
Инструкция
1. Нужно разобраться, как дозволено вычислить площадь начальной трапеции . Для этого существуют несколько формул, в зависимости от начальных данных:S = ((a+b)*h)/2, где a и b – длины оснований трапеции , а h – ее высота (Высота трапеции – перпендикуляр, опущенный от одного основания трапеции к иному);S = m*h, где m – средняя линяя трапеции (Средняя линяя – отрезок, параллельный основаниями трапеции и соединяющий середины ее боковых сторон).
2. Сейчас, зная формулы для исчисления площади трапеции , дозволено из них вывести новые, для нахождения высоты трапеции :h = (2*S)/(a+b);h = S/m.
3. Для того, дабы было внятнее, как решать сходственные задачи, дозволено разглядеть примеры:Пример 1: Дана трапеция, у которой площадь равна 68 см?, средняя линяя которой равна 8 см, требуется обнаружить высоту данной трапеции . Для того, дабы решить данную задачу, требуется воспользоваться ранее выведенной формулой:h = 68/8 = 8.5 смОтвет: высота данной трапеции составляет 8.5 смПример 2: Пускай у трапеции площадь равняется 120 см?, длины оснований данной трапеции равны 8 см и 12 см соответственно, требуется обнаружить высоту этой трапеции . Для этого нужно применить одну из выведенных формул:h = (2*120)/(8+12) = 240/20 = 12 смОтвет: высота заданной трапеции равна 12 см
Видео по теме
Обратите внимание!
Любая трапеция владеет рядом свойств:- средняя линяя трапеции равна полусумме ее оснований;- отрезок, тот, что соединяет между собой диагонали трапеции, равен половине разности его оснований;- если через середины оснований провести прямую, то она пересечет точку пересечения диагоналей трапеции;- в трапецию дозволено вписать окружность в том случае, если сумма оснований данной трапеции равна сумме ее боковых сторон.Пользуйтесь этими свойствами при решении задач.
Совет 4: Как обнаружить высоту треугольника, если даны координаты точек
Высотой в треугольнике называют отрезок прямой линии, соединяющий вершину фигуры с противолежащей стороной. Данный отрезок непременно должен быть перпендикулярен стороне, следственно из всякой вершины дозволено провести лишь одну высоту . От того что вершин в этой фигуре три, высот в нем столько же. Если треугольник задан координатами своих вершин, вычисление длины всякой из высот дозволено произвести, скажем, воспользовавшись формулой нахождения площади и рассчитав длины сторон.

Инструкция
1. Исходите в расчетах из того, что площадь треугольника равна половине произведения длины всякий из его сторон на длину высоты, опущенной на эту сторону. Из этого определения вытекает, что для нахождения высоты надобно знать площадь фигуры и длину стороны.
2. Начните с вычисления длин сторон треугольника . Обозначьте координаты вершин фигуры так: A(X?,Y?,Z?), B(X?,Y?,Z?) и C(X?,Y?,Z?). Тогда длину стороны AB вы сумеете рассчитать по формуле AB = ?((X?-X?)? + (Y?-Y?)? + (Z?-Z?)?). Для 2-х других сторон эти формулы будут выглядеть так: BC = ?((X?-X?)? + (Y?-Y?)? + (Z?-Z?)?) и AC = ?((X?-X?)? + (Y?-Y?)? + (Z?-Z?)?). Скажем, для треугольника с координатами A(3,5,7), B(16,14,19) и C(1,2,13) длина стороны AB составит ?((3-16)? + (5-14)? + (7-19)?) = ?(-13? + (-9?) + (-12?)) = ?(169 + 81 + 144) = ?394 ? 19,85. Длины сторон BC и AC, рассчитанные таким же методом, будут равны ?(15? + 12? + 6?) = ?405 ? 20,12 и ?(2? + 3? + (-6?)) = ?49 = 7.
3. Умения длин 3 сторон, полученных на предыдущем шагу, довольно для вычисления площади треугольника (S) по формуле Герона: S = ? * ?((AB+BC+CA) * (BC+CA-AB) * (AB+CA-BC) * (AB+BC-CA)). Скажем, позже подстановки в эту формулу значений, полученных из координат треугольника -примера из предыдущего шага, эта формула даст такое значение: S = ?*?((19,85+20,12+7) * (20,12+7-19,85) * (19,85+7-20,12) * (19,85+20,12-7)) = ?*?(46,97 * 7,27 * 6,73 * 32,97) ? ?*?75768,55 ? ?*275,26 = 68,815.
4. Исходя из площади треугольника , рассчитанной на предыдущем шаге, и длин сторон, полученных на втором шаге, вычислите высоты для всякой из сторон. Потому что площадь равна половине произведения высоты на длину стороны, к которой она проведена, для нахождения высоты разделяете удвоенную площадь на длину надобной стороны: H = 2*S/a. Для использованного выше примера высота, опущенная на сторону AB составит 2*68,815/16,09 ? 8,55, высота к стороне ВС будет иметь длину 2*68,815/20,12 ? 6,84, а для стороны АС эта величина будет равна 2*68,815/7 ? 19,66.






