Совет 1: Как обнаружить норму матрицы

Матрица – основа всякий математической модели, будь то решение системы уравнений либо задачи линейного программирования. Дабы обнаружить норму матрицы , необходимо реально получить действительное число по определенной схеме.

Инструкция

1. Представление нормы универсально для всякий матрицы , квадратной либо неквадратной, матрицы -столбца либо строки, размерность также может быть всякий. Эта колляцию применяют в качестве оценочной величины для обзора изменяемости матрицы в каком-нибудь расчетном процессе либо общности нескольких матриц.

2. Дозволено сказать, что норма является показателем «мощности» матрицы . Она обозначается ?A? и равна действительному числу, которое должно соответствовать определенному комплекту условий:?А? ? 0, причем равенство нулю выполняется только для нулевой матрицы ;?а•А? = ?а?•?А?, где а принадлежит множеству разумных чисел;?А+В? ? ?А? + ?В? – коммутативность.

3. Норма, для которой выполняется также качество ?А•В? ? ?А? • ?В?, именуется мультипликативной. Существует три вида норм: безграничная, первая и евклидова. Все они являются каноническими, т.е. их значения не поменьше по модулю всякого матричного элемента. На практике традиционно вычисляют только один из видов, этого довольно для объективной оценки.

4. Дабы обнаружить норму матрицы , надобно воспользоваться одним из ниже приведенных методов для всего вида. Все они основаны на расчете суммы элементов матрицы , но весь подразумевает личный алгорифм.

5. Для расчета безмерной нормы просуммируйте по модулю значения элементов отдельно по всякой строке и выберите из них наивысшее:?A?_1 = mах_i ?_j |а_ij|.

6. Обнаружьте первую норму , поступив подобно с элементами по всем столбцу:?A?_2 = mах_j ?_i |а_ij|.

7. Расчет евклидовой нормы подразумевает три действия: возведение всякого элемента в квадрат, суммирование и извлечение квадратной корня из всеобщего итога:?A?_3 = ??а?_ij.

8. Пример: вычислите все виды норм для данной матрицы .



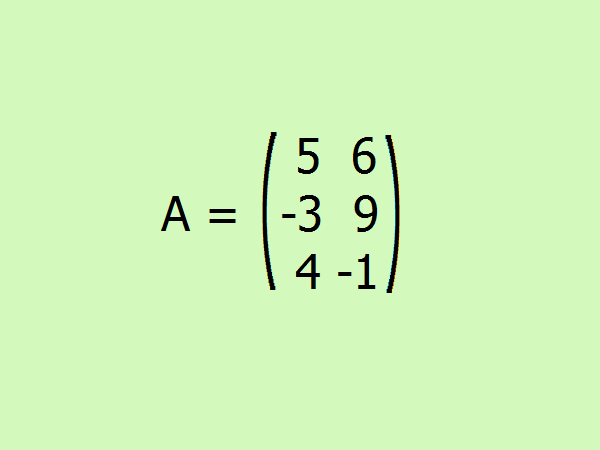
9. Решениеa11+a12=11; a21+a22=12; a31+a32=5 ? ?А?_1 = 12;a11+a21+a31=12; a12+a22+32=16 ? ?А?_2 = 16;?А?_3 = ?(25+36+9+81+16+1) = ?168 ? 13.

Совет 2: Как привести матрицу к каноническому виду

Матрицы – комфортный инструмент для решения самых разных алгебраических задач. Умение некоторых примитивных правил для оперирования с ними дозволяет приводить матрицы к любым комфортным и нужным в данный момент формам. Зачастую пригодным является применение канонической формы матрицы.

Инструкция

1. Запомните, что канонический вид матрицы не требует, дабы на каждой основной диагонали стояли единицы. Суть определения заключается в том, что исключительные ненулевые элементы матрицы в ее каноническом виде – это единицы. Если они присутствуют, то располагаются на основной диагонали. При этом их число может варьироваться от нуля до числа строчек в матрице.

2. Не забывайте, что элементарные реформирования разрешают всякую матрицу привести к каноническому виду . Самая огромная трудность – подсознательно обнаружить особенно примитивную последовательность цепочек действий и не ошибиться в вычислениях.

3. Выучите основные свойства операций со строчками и столбцами в матрице. К элементарным реформированиям относят три стандартных реформирования. Это умножение строчки матрицы на всякое ненулевое число, суммирование строк (в том числе прибавление к одной иной, умноженной на какое-то число) и их перегруппировка. Сходственные действия дозволяют получить матрицу равнозначную данной. Соответственно, вы можете исполнить такие операции и со столбцами без потери эквивалентности.

4. Усердствуйте не исполнять единовременно сразу несколько элементарных реформирований: продвигайтесь от этапа к этапу, дабы не допустить случайной ошибки.

5. Обнаружьте статус матрицы, дабы определить число единиц на основной диагонали: это подскажет вам, какой окончательный вид будет иметь желанная каноническая форма, и избавит от необходимости исполнять реформирования, если требуется легко применять ее для решения.

6. Воспользуйтесь способом окаймляющих миноров для того, дабы исполнить предыдушую рекомендацию. Вычислите минор к-ого порядка, а также все окаймляющие его миноры степени (к+1). Если они равны нулю, то статус матрицы есть число к. Не забывайте, что минор Мij – это определитель матрицы, получаемой при вычеркивании строки i и столбца j из начальной.

Совет 3: Как обнаружить всеобщее решение системы

Минимальное число переменный, которое может содержать система уравнений, равно двум. Обнаружить всеобщее решение систему – это значит обнаружить такое значение х и у, при поставлении которых в всякое уравнение будут получаться правильные равенства.

Инструкция

1. Есть несколько методов решить либо, по крайней мере, упростить систему уравнений. Дозволено перенести всеобщий множитель за скобку, вычесть либо сложить уравнения системы , дабы получить новое упрощенное равенство, но самый легкой метод – выразить одну переменную через иную и решить уравнения поочередно.

2. Возьмите систему уравнений:2х-y+1=5;x+2y-6=1.Из второго уравнения системы выразите х, перенеся остальные члены выражения в правую сторону за знак равенства. Нужно помнить, что при этом знаки, стоящие при них, нужно сменить на противоположные, то есть “+” на “-” и напротив:х=1-2у+6;х=7-2у.

3. Подставьте это выражение в первое уравнение системы взамен х:2*(7-2у)-у+1=5.Раскройте скобки:14-4у-у+1=5.Произведите сложение равных величин – свободных чисел и показателей при переменной:-5у+15=5.Перенесите свободные числа за знак равенства:-5у=-10.

4. Обнаружьте всеобщий множитель, равный показателю при переменной у (тут он будет равняться -5): у=2.Подставьте получившееся значение в упрощенное уравнение:х=7-2у;х=7-2*2=3.Таким образом, получается, что всеобщим решение м системы является точка с координатами (3;2).

5. Еще один метод решить данную систему уравнений заключается в распределительном свойстве сложения, а также законе умножения обоих частей уравнения на целое число:2х-y+1=5;x+2y-6=1.Умножьте второе уравнение на 2:2х+4у-12=2.Из первого уравнения вычтите второе:2х-2х-у-4у+1+13=5-2.

6. Таким образом избавьтесь от переменной х:-5у+13=3.Перенесите числовые данные в правую сторону равенства, меняя при этом знак:-5у=-10;Получается у=2.Подставьте полученное значение в всякое уравнение системы и получите х=3.

Видео по теме

Совет 4: Как обнаружить личные числа матрицы

Матрицы, представляющие собой табличную форму записи данных, обширно используются при работе с системами линейных уравнений. Причем число уравнений определяет число строк матрицы, а число переменных – порядок ее столбцов. В итоге решение линейных систем сводится к операциям над матрицами, одна из которых – поиск собственных чисел матрицы. Их вычисление осуществляется с подмогой характеристического уравнения. Личные числа могут быть определены для квадратной матрицы порядка m.

Инструкция

1. Запишите заданную квадратную матрицу А. Для поиска ее собственных чисел используйте характеристическое уравнение, вытекающее из данные нетривиального решения линейной однородной системы, представленной в данном случае квадратной матрицей. Как следует из правила Крамера, решение существует только в том случае, если ее определитель равен нулю. Таким образом, дозволено записать уравнение | A – ?E | = 0, где А – заданная матрица, ? – желанные личные числа, E – единичная матрица, у которой все элементы на основной диагонали равны единице, а остальные – нулю.

2. Исполните умножение желанной переменной ? на единичную матрицу Е той же размерности, что и заданная начальная А. Итогом операции будет являться матрица, где по основной диагонали расположены значения ?, остальные элементы остаются равными нулю.

3. Вычтите из заданной матрицы А полученную в предыдущем шаге матрицу. Результирующая матрица разности будет повторять начальную А за исключением элементов по основной диагонали. Они же будут представлять собой разность: (аii – ?), где аii – элементы основной диагонали матрицы А, ? – переменная, определяющая желанные личные числа.

4. Обнаружьте определитель полученной матрицы разности. В случае рассмотрения системы второго порядка он равен разности произведений элементов основной и побочной диагонали матрицы: (а11 – ?)*( а22 – ?) – а12* а21. Для третьего порядка вычисление определителя проводится по правилу Саррюса (правилу треугольников): а11*а22*а33 + а13*а21*а32 + а12*а23*а31 – а21*а12*а33 – а13*а22*а31 – а11*а32*а23, где аij – элементы матрицы. При решении матриц большей размерности уместно применять способ Гаусса либо разложение по строке.

5. В итоге вычислений определителя и проведенных облегчений получится линейное уравнение с незнакомой переменной ?. Решите уравнение. Все его действительные корни и будут являться собственными числами начальной матрицы А.