Совет 1: Как выразить синус через косинус

Тригонометрия – один из любимых разделов алгебры для всех, кто любит справляться с уравнениями, исполнять заботливые реформирования, владеет наблюдательностью и терпением. Умение основных теорем и формул дозволяет находить не только верное, но и особенно прекрасное решение многих задач, в том числе физических либо геометрических. Даже легко выразив синус через косинус , вы можете натолкнуться на решение.

Инструкция

1. Воспользуйтесь умениями планиметрии, дабы выразить синус через косинус . Согласно определению, синус ом угла в прямоугольном треугольнике именуется отношение длины противолежащего катета к гипотенузе, а косинус ом – прилежащего катета к гипотенузе. Даже умение примитивный теоремы Пифагора дозволит вам в некоторых случаях стремительно обнаружить желанное реформирование.

2. Выразите синус через косинус , воспользовавшись простейшим тригонометрическим тождеством, согласно которому сумма квадратов этих величин дает единицу. Обратите внимание, что правильно исполнить задание вы сумеете, только если знаете, в какой четверти находится желанный угол, в отвратном случае вы получите два допустимых итога – с позитивным и негативным знаком.

3. Запомните формулы приведения, также разрешающие осуществить нужную операцию. Согласно им, если к числу ?/2 прибавить (либо отнять от него) угол а, то образуется косинус этого угла. Те же операции с числом 3?/2 дают косинус , взятый с негативным знаком. Соответственно, в случае, если вы трудитесь с косинус ом, то синус вам дозволит получить прибавление либо вычитание из 3?/2, а его негативное значение – из ?/2.

4. Воспользуйтесь формулами для нахождения синус а либо косинус а двойного угла, дабы выразить синус через косинус . Синус двойного угла есть удвоенное произведение синус а и косинус а этого угла, а косинус удвоенного угла – разность между квадратами косинус а и синус а.

5. Обратите внимание и на вероятность обращения к формулам суммы и разности синус ов и косинус ов 2-х углов. Если вы исполняете операции с углами а и с, то синус их суммы (разности) – это сумма (разность) произведения синус ов этих углов и их косинус ов, а косинус суммы (разности) есть разность (сумма) произведения косинус ов и синус ов углов, соответственно.

Совет 2: Как находить косинус в треугольнике

Часто в геометрических (тригонометрических) задачах требуется обнаружить косинус угла в треугольнике , так как косинус угла дозволяет однозначно определить величину самого угла.

Инструкция

1. Дабы обнаружить косинус угла в треугольнике , длины сторон которого знамениты, дозволено воспользоваться теоремой косинус ов. Согласно этой теореме, квадрат длины стороны произвольного треугольника равняется сумме квадратов 2-х его других сторон без удвоенного произведения длин этих сторон на косинус угла между ними:а?=b?+c?-2*b*c*соs?, где:а, b, с – стороны треугольника (вернее их длины),? – угол, противоположный стороне а (его величина).Из приведенного равенства легко находится соs?:соs?=( b?+c?-а? )/(2*b*c)Пример 1.Имеется треугольник со сторонами а, b, с, равными 3, 4, 5 мм, соответственно.Обнаружить косинус угла, заключенного между крупными сторонами.Решение:По условию задачи имеем:а=3,b=4,с=5.Обозначим противоположный стороне а угол через ?, тогда, согласно выведенной выше формуле, имеем:соs?=(b?+c?-а? )/(2*b*c)=(4?+5?-3?)/(2*4*5)=(16+25-9)/40=32/40=0,8Ответ: 0,8.

2. Если треугольник прямоугольный, то для нахождения косинус а угла довольно знать длины каждого 2-х всяких сторон (косинус прямого угла равен 0).Пускай имеется прямоугольный треугольник со сторонами а, b, с, где с – гипотенуза.Разглядим все варианты:Пример 2.Обнаружить соs?, если знамениты длины сторон а и b (катеты треугольника)Воспользуемся добавочно теоремой Пифагора:c?=b?+а?,с=v(b?+а?)соs?=(b?+c?-а? )/(2*b*c)=(b?+b?+а?-а?)/(2*b*v(b?+а?))=(2*b?)/(2*b*v(b?+а?))=b/v(b?+а?)Дабы проверить правильность полученной формулы, подставим в нее значения из примера 1, т.е.а=3,b=4.Проделав элементарные вычисления, получаем:соs?=0,8.

3. Подобно находится косинус в прямоугольном треугольнике в остальных случаях:Пример 3.Вестимы а и с (гипотенуза и противолежащий катет), обнаружить соs?b?=с?-а?,b=v(c?-а?)соs?=(b?+c?-а? )/(2*b*c)=(с?-а?+с?-а?)/(2*с*v(с?-а?))=(2*с?-2*а?)/(2*с*v(с?-а?))=v(с?-а?)/с.Подставляя значения а=3 и с=5 из первого примера, получаем:соs?=0,8.

4. Пример 4.Вестимы b и с (гипотенуза и прилежащий катет).Обнаружить соs?Произведя схожие (показанные в примерах 2 и 3 реформирования), получим, что в этом случае косинус в треугольнике вычисляется по дюже легкой формуле:соs?=b/с.Простота выведенной формулы объясняется элементарно: реально, прилежащий к углу ? катет является проекцией гипотенузы, следственно его длина равна длине гипотенузы, умноженной на соs?.Подставляя значения b=4 и с=5 из первого примера, получим:соs?=0,8Значит, все наши формулы правильны.

Совет 3: Как обнаружить косинус, зная синус

Для того дабы получить формулу, объединяющую синус и косинус угла, нужно дать либо припомнить некоторые определения. Так, синус угла – это отношение (частное от деления) противолежащего катета прямоугольного треугольника к гипотенузе. Косинус угла – это отношение прилежащего катета к гипотенузе.

Инструкция

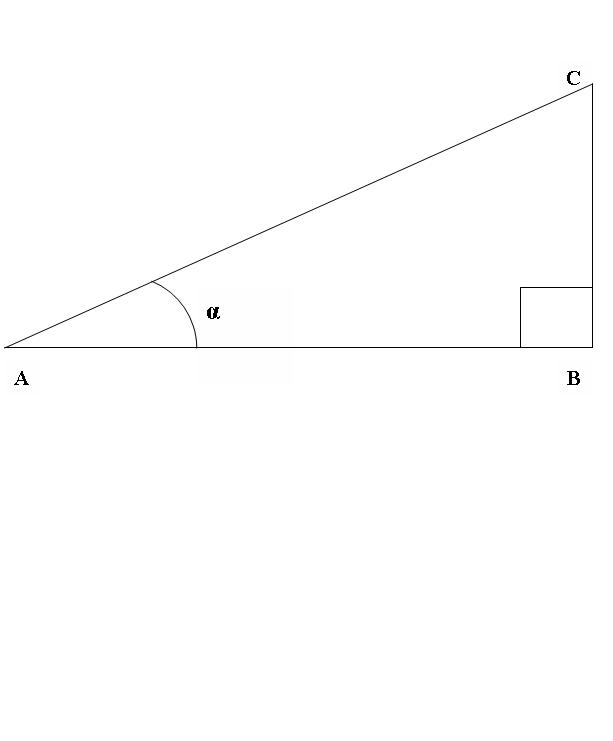
1. Нарисуем прямоугольный треугольник АВС, где угол АВС – прямой (рис.1). Разглядим соотношение синус а и косинус а угла САВ. По данному выше определениюsin CAB=BC/AC, cos CAB=AB/AC.

2. Припоминаем теорему Пифагора – АВ^2 + BC^2 = AC^2, где ^2 – операция возведения в квадрат.Поделим левую и правую части уравнения на квадрат гипотенузы AC. Тогда предыдущее равенство будет выглядеть так:АВ^2/AC^2 + BC^2/AC^2 = 1.

3. Для комфорта перепишем равенство, полученное на шаге 2, дальнейшим образом:(AB/AC)^2 + (BC/AC)^2 = 1.Согласно определениям, данным на шаге 1, получаем:cos^2(CAB) + sin^2(CAB) = 1, т.е.cos(CAB)=SQRT(1-sin^2(CAB)), где SQRT – операция взятия квадратного корня.

Полезный совет
Величина синуса и косинуса всякого угла не может быть огромнее 1.

Совет 4: Как обнаружить косинус, если знаменит синус

Синус и косинус – это прямые тригонометрические функции, для которых существует несколько определений – через окружность в декартовой системе координат, через решения дифференциального уравнения, через острые углы в прямоугольном треугольнике. Всякое из таких определений дозволяет вывести связанность между этими двумя функциями. Ниже приведен самый, вероятно, примитивный метод выразить косинус через синус – через их определения для острых углов прямоугольного треугольника.

Инструкция

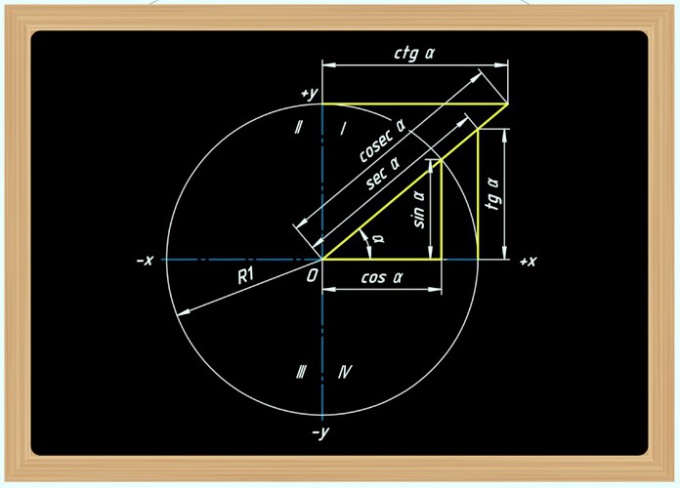
1. Выразите синус острого угла прямоугольного треугольника через длины сторон этой фигуры. Согласно определению, синус угла (?) должен быть равен отношению длины стороны (a), лежащей наоборот него – катета – к длине стороны (c), противолежащей прямому углу – гипотенузы: sin(?) = a/c.

2. Обнаружьте аналогичную формулу для косинус а того же угла. По определению эта величина должна выражаться отношением длины стороны (b), примыкающей к этому углу (второго катета), к длине стороны (c), лежащей наоборот прямого угла: cos(а) = a/c.

3. Перепишите равенство, вытекающее из теоремы Пифагора, таким образом, дабы в нем были задействованы соотношения между катетами и гипотенузой, выведенные на 2-х предыдущих шагах. Для этого вначале поделите обе части начального уравнения этой теоремы (a? + b? = c?) на квадрат гипотенузы (a?/c? + b?/c? = 1), а после этого полученное равенство перепишите в таком виде: (a/c)? + (b/c)? = 1.

4. Замените в полученном выражении соотношения длин катетов и гипотенузы тригонометрическими функциями, исходя из формул первого и второго шага: sin?(а) + cos?(а) = 1. Выразите косинус из полученного равенства: cos(a) = ?(1 – sin?(а)). На этом задачу дозволено считать решенной в всеобщем виде.

5. Если помимо всеобщего решения надобно получить численный итог, воспользуйтесь, скажем, калькулятором, встроенным в операционную систему Windows. Ссылку на его запуск обнаружьте в подразделе «Типовые» раздела «Все программы» основного меню ОС. Эта ссылка сформулирована немногословно – «Калькулятор». Дабы иметь вероятность вычислять с поддержкой этой программы тригонометрические функции включите ее «инженерный» интерфейс – нажмите комбинацию клавиш Alt + 2.

6. Введите данное в условиях значение синуса угла и кликните по кнопке интерфейса с обозначением x? – так вы построите начальное значение в квадрат. После этого наберите на клавиатуре *-1, нажмите Enter, введите +1 и нажмите Enter еще раз – таким методом вы вычтите из единицы квадрат синуса. Щелкните по клавише со значком радикала, дабы извлечь квадратный корень и получить окончательный итог.

Совет 5: Как обнаружить синус, зная угол

Одной из фундаментальных основ точных наук является представление о тригонометрических функциях. Они определяют примитивные отношения между сторонами прямоугольного треугольника. К семейству данных функций относится синус. Обнаружить его, зная угол, дозволено огромным числом методов, включающих экспериментальные, вычислительные способы, а также применение справочной информации.



Вам понадобится

• – калькулятор;
• – компьютер;
• – электронные таблицы;
• – таблицы брадиса;
• – бумага;
• – карандаш.

Инструкция

1. Используйте калькулятор с функцией вычисления синуса для приобретения необходимых значений на основании познания угла. Сходственный функционал сегодня имеют даже самые примитивные устройства. При этом вычисления производятся с дюже высокой степенью точности (как водится, до восьми и больше знаков позже запятой).

2. Примените программное обеспечение, представляющее собой среду для работы с электронными таблицами, запущенное на персональном компьютере. Примерами сходственных приложений являются Microsoft Office Excel и OpenOffice.org Calc. Введите в всякую ячейку формулу, состоящую из вызова функции вычисления синуса с необходимым доводом. Нажмите Enter. В ячейке отобразится желанная величина. Превосходством электронных таблиц является вероятность стремительного расчета значений функций для большого комплекта доводов.

3. Узнайте приближенное значение синуса угла из таблиц Брадиса, если они имеются в наличии. Их недостатком является точность значений, ограниченная четырьмя знаками позже запятой.

4. Обнаружьте приближенное значение синуса угла, совершив геометрические построения. На листе бумаги вычертите отрезок. При помощи транспортира отложите от него угол, синус которого нужно обнаружить. Начертите еще один отрезок, пересекающий 1-й в некоторой точке. Перпендикулярно первому же отрезку проведите прямую линию, пересекающую два теснее существующих отрезка. Получится прямоугольный треугольник. Измерьте длину его гипотенузы и катета, противолежащего углу, построенному при помощи транспортира. Поделите второе значение на первое. Это и будет желанная величина.

5. Рассчитайте синус угла, применяя разложение в ряд Тейлора. Если значение угла представлено в градусах, переведите его в радианы. Используйте формулу вида: sin(х) = х – (х^3)/3! + (х^5)/5! – (х^7)/7! + (х^9)/9! – … Для возрастания скорости расчетов записывайте нынешнее значение числителя и знаменателя последнего члена ряда, производя вычисление дальнейшего значения на основе предыдущего. Увеличивайте длину ряда для приобретения больше точной величины.

Видео по теме

Совет 6: Что такое синус и косинус

Постижение треугольников ведется математиками на протяжении нескольких тысячелетий. Наука о треугольниках – тригонометрия – использует особые величины: синус и косинус.

Прямоугольный треугольник

Изначально синус и косинус появились из-за необходимости рассчитывать величины в прямоугольных треугольниках. Было подмечено, что если значение градусной меры углов в прямоугольном треугольнике не менять, то соотношение сторон, насколько бы эти стороны ни изменялись в длине, остается неизменно идентичным.Именно так и были введены представления синуса и косинуса. Синус острого угла в прямоугольном треугольнике – это отношение противолежащего катета к гипотенузе, а косинус – прилежащего к гипотенузе.

Теоремы косинусов и синусов

Но косинусы и синусы могут использоваться не только в прямоугольных треугольниках. Дабы обнаружить значение тупого либо острого угла, стороны всякого треугольника, довольно применить теорему косинусов и синусов.Теорема косинусов достаточно примитивна: «Квадрат стороны треугольника равен сумме квадратов 2-х других сторон за вычетом удвоенного произведения этих сторон на косинус угла между ними». Существует две трактовки теоремы синусов: малая и расширенная. Согласно малой: «В треугольнике углы пропорциональны противолежащим сторонам». Данную теорему зачастую расширяют за счет свойства описанной около треугольника окружности: «В треугольнике углы пропорциональны противолежащим сторонам, а их отношение равно диаметру описанной окружности».

Производные

Производная – математический инструмент, показывающий, как стремительно меняется функция касательно метаморфозы ее довода. Производные применяются в алгебре, геометрии, экономике и физике, ряде технических дисциплин. При решении задач требуется знать табличные значения производных тригонометрических функций: синуса и косинуса. Производной синуса является косинус, а косинуса – синус, но со знаком «минус».

Применение в математике

Особенно зачастую синусы и косинусы применяются при решении прямоугольных треугольников и задач, связанных с ними. Удобство синусов и косинусов обнаружило свое отражение и в технике. Углы и стороны было примитивно оценивать по теоремам косинусов и синусов, разбивая трудные фигуры и объекты на «примитивные» треугольники. Инженеры и архитекторы, зачастую имеющие дело с расчетами соотношения сторон и градусных мер, тратили много времени и усилий для вычисления косинусов и синусов не табличных углов. Тогда «на подмогу» пришли таблицы Брадиса, содержащие тысячи значений синусов, косинусов, тангенсов и котангенсов различных углов. В советское время некоторые преподаватели принуждали своих подопечных учить страницы таблиц Брадиса назубок.