Совет 1: Как вычислить площадь поперечного сечения

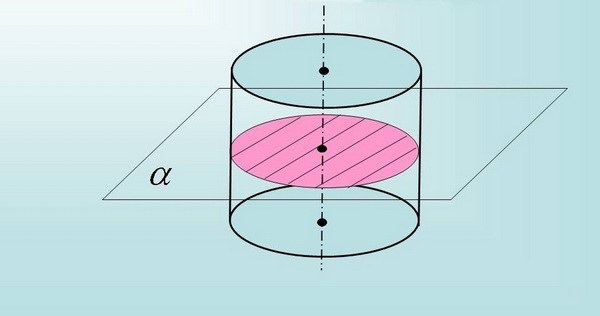
Поперечное сечение образуется под прямым углом по отношению к продольной оси. Причем, сечение различных геометрических фигур представлено может быть разными формами. К примеру, у параллелограмма сечение по внешнему виду напоминает прямоугольник либо квадрат, у цилиндра – прямоугольник либо круг и т.д.



Вам понадобится

• – калькулятор;
• – начальные данные.

Инструкция

1. Дабы обнаружить площадь сечения параллелограмма, надобно знать значение его основания и высоту. Если, к примеру, знаменита лишь длина и ширина основания, то обнаружьте диагональ, применяя для этого теорему Пифагора (квадрат длины гипотенузы в прямоугольном треугольнике равен сумме квадратов катетов: a2 + b2 = c2). Ввиду этого, c = sqrt (a2 + b2).

2. Обнаружив значение диагонали, подставьте его в формулу S= c*h, где h – высота параллелограмма. Полученный итог и будет величиной площадью поперечного сечения параллелограмма.

3. Если же сечение проходит по 2-х оснований, то его площадь рассчитывайте по формуле: S=a*b.

4. Для вычисления площади осевого сечения цилиндра, проходящей перпендикулярно основаниям (при условии, что одна сторона этого прямоугольника равна радиусу основания, а вторая – высоте цилиндра), используйте формулу S =2R*h, в которой R – величина радиуса окружности (основания), S – площадь поперечного сечения, а h – высота цилиндра.

5. Если по условиям задачи сечение не проходит через ось вращения цилиндра, но при этом параллельно его основаниям, значит, сторона прямоугольника не будет равна диаметру окружности основания.

6. Независимо вычислите незнакомую сторону путем построения окружности основания цилиндра, проведения перпендикуляров от стороны прямоугольника (плоскости сечения) к окружности и расчета размера хорды (по теореме Пифагора). Позже этого подставьте в S =2а*h полученное значение (2а – значение хорды) и рассчитайте площадь поперечного сечения.

7. Площадь сечения шара определяется по формуле S = ?R2. Обратите внимание на то, что, если расстояние от центра геометрической фигуры до плоскости будет совпадать с плоскостью, то площадь сечения равна будет нулю, потому как шар касается плоскости лишь в одной точке.

Совет 2: Как лечить плоскостопие поперечное

Если внезапно вы начали примечать, что увеличились косточки на огромных пальцах ног, что вам больно носить обувь (исключительно летом), это обозначает, что у вас поперечное плоскостопие . В таком случае нужно сразу же обратиться к врачу-ортопеду. Не медлите, чай чем прежде начнется лечение, тем отличнее.

Инструкция

1. Эксперт проведет осмотр и порекомендует вам один из основных способов лечения поперечного плоскостопия. 1-й из них – консервативный, он подходит только для лечения первой степени болезни. Сам способ заключается в снижении веса, уменьшении статической нагрузки, отказе от “каблуков” и неудобной обуви. Помимо того, при консервативном лечении пациенту назначаются физиотерапевтические процедуры, целебная физкультура, массаж. Доктор также может порекомендовать ношение стелек со особыми ортопедическими валиками.

2. Иной способ (оперативный) используется для лечения поперечного плоскостопия 2-й и третьей степени. Входящих в него вариаций насчитывается больше четырехсот, впрочем, ни одна из них не устраняет основную причину возникновения болезни – слабость мышечно-связочного агрегата. В крайнем случае может понадобиться хирургическое ввязывание, то есть пересадка сухожилий мышц либо пластика капсулы суставов. Позже такой операции пациент должен носить обувь только с индивидуальными стельками и со стельками с валиком Зейтца, а также с супинаторами.

3. Не стоит отказываться и от рецептов народной медицины. Вот один из них: возьмите 10-ти % раствор йода и нанесите его на косточку большого пальца. Это поможет снять воспаление и остановит рост хрящевой ткани. Правда, будьте осмотрительны с йодом, не используйте мощно концентрированный раствор, напротив вы рисуете получить ожог кожи. Такую же рекомендацию дозволено дать и к компрессам с добавлением уксусной эссенции. Кстати, современная медицина предлагает огромный выбор мазей, гелей, способных снять воспаление суставов и усовершенствовать питание тканей. Впрочем не приобретайте сходственные средства самосильно, посоветуйтесь с лечащим врачом.

Полезный совет
Усердствуйте не находиться в обуви слишком длинно, давайте ногам передохнуть. Стоит подметить, что приобретаемая вам обувь должна быть комфортной и “дышащей”.

Совет 3: Сечение параллелепипеда: как рассчитать его площадь

Масса задач составлена на основе свойств многогранников. Грани объёмных фигур, как и определенные точки на них, лежат в различных плоскостях. Если одну из таких плоскостей под определённым углом провести через параллелепипед, то часть плоскости, лежащая в пределах многогранника и разделяющая его на части, будет его сечением .



Вам понадобится

• – линейка
• – карандаш

Инструкция

1. Постройте параллелепипед. Помните, что его основание и всякая из граней обязаны представлять собой параллелограмм. Это обозначает, что вам нужно возвести многогранник так, дабы все противоположные рёбра параллельны. Если в условии сказано возвести сечение прямоугольного параллелепипеда , то его грани сделайте прямоугольными. У прямой параллелепипед прямоугольные только 4 боковые грани. Если боковые грани параллелепипеда не перпендикулярны основанию, то такой многогранник называют наклонным. Если вы хотите возвести сечение куба, первоначально начертите прямоугольный параллелепипед с равными размерами. Тогда все шесть его граней будут представлять собой квадраты. Назовите все вершины для комфорта обозначения.

2. Обозначьте две точки, которые будут принадлежать плоскости сечения. Изредка их расположение указано в задаче: расстояние от ближайшей вершины, конец отрезка, проведённого по определенным условиям. Сейчас проведите прямую через точки, лежащие в одной плоскости.

3. Обнаружьте прямые на пересечении секущей плоскости с гранями параллелепипеда . Для выполнения этого шага обнаружьте точки, в которых прямая, лежащая в плоскости сечения параллелепипеда , пересекается с прямой линией, принадлежащей грани параллелепипеда . Эти прямые обязаны находиться в одной плоскости.

4. Достройте сечение параллелепипеда . При этом помните, что ее плоскость должна пересекать параллельные грани параллелепипеда по параллельным прямым.

5. Стройте секущую плоскость в соответствии с начальными данными в задаче. Существует несколько вероятностей построения плоскости сечения, проходящей:- перпендикулярно заданной прямой линии через заданную точку;- перпендикулярно заданной плоскости через заданную прямую;- параллельно двум скрещивающимся прямым через заданную точку;- параллельно иной заданной прямой через иную заданную прямую;- параллельно заданной плоскости через заданную точку.По таким начальным данным стройте сечение по тезису, описанному выше.

Видео по теме


Обратите внимание!
Дабы возвести сечение параллелепипеда, необходимо определить точки пересечения плоскости сечения с ребрами параллелепипеда, а после этого объединить данные точки отрезками. Учтите, что соединять только те точки, которые лежат в плоскости одной грани. Параллельные грани параллелепипеда пересекайте секущей плоскостью по параллельным отрезкам. Если в плоскости грани только одна точка принадлежит плоскости сечения, постройте дополнительную такую точку. Для этого обнаружьте точки пересечения построенных прямых с теми прямыми, которые лежат в необходимых гранях.

Полезный совет
Параллелепипед имеет 6 граней. В его сечениях могут получиться треугольники, четырёхугольники, пятиугольники и фигуры с шестью углами. Плоскость, в том числе и секущая, определяется:- тремя точками;- прямой линией и одной точкой;- двумя линиями, параллельными друг другу;- двумя прямыми, пересекающимися между собой.

Совет 4: Как вычислить дирекционный угол

Ориентирование в полевых условиях главная составляющая многих профессий. Для этого применяют карты и компасы. Для определения направления по карте на определенный объект применяют дирекционный угол и магнитные азимуты.



Вам понадобится

• Компас либо буссоль, остро наточенный карандаш, линейка, транспортир.

Инструкция

1. Дирекционным углом в геодезии называют угол между линией проходящей через данную точку направлением на цель и линией параллельной оси абсцисс, отчитываемой от северного направления оси абсцисс. Его отсчитывают слева на права (по ходу стрелки) от 0о до 360°.

2. Комфортнее каждого определять дирекционный угол по карте. Карандашом, по линейке, прочертите линию через центры условных знаков отправного пункта и ориентира. Длина проведенной линии, для комфорта измерения, должна превышать радиус транспортира. Позже этого, совместите центр транспортира с точкой пересечения линий и поверните его так, дабы нуль на транспортире совпадал с вертикальной линией сетки на карте (либо линией ей параллельной). Значения угла отсчитывайте по направлению хода часовой стрелки. Средняя оплошность измерения дирекционного угла транспортиром составляет от 15/ до 1о.

3. Изредка, для вычисления дирекционных углов применяют магнитные азимуты. Магнитный азимут – это плоский горизонтальный угол образованный линией направленной на цель и северным направлением магнитного меридиана. Он отсчитывает также от 0о до 360о по ходу часовой стрелки. Магнитные азимуты измеряют на местности с подмогой компаса либо буссоли. Стрелка компаса, вернее ее магнитное поле, взаимодействует с магнитным полем местности и показывает направление магнитного меридиана.

4. Дальше нужно определить поправку направления (сумму сближения меридианов и магнитного склонения). Магнитным склонением называют угол между магнитными и географическими меридианами в заданной точке. Сближение меридианов это угол между касательной, проведенной к меридиану данной точки и касательной к поверхности эллипсоида вращения, проведенной в той же точке, параллельно исходному меридиану. Поправка направления также отсчитывается также от северного направления координатной сетки по направлению хода часовой стрелки. Поправку направления принято считать позитивной, если стрелка отклоняется вправо (на восток) и негативной, если отклоняется налево (на запад). Измеренный с поддержкой буссоли на местности магнитный азимут дозволено перевести в дирекционный угол прибавив к нему поправку направления, наблюдательно рассматривая знак поправки.

Обратите внимание!
На многих картах зачастую указывают значения сближения меридианов (его еще называют Гауссово сближение)и поправки направления

Полезный совет
Обращайте специальное внимание на направление отсчета и рассматривайте все знаки.

Совет 5: Как вычислить площадь параллелограмма

Параллелограмм – это выпуклая четырехугольная геометрическая фигура, в которой пары противоположных сторон имеют идентичную длину. Также и пары углов в противоположных вершинах имеют идентичные величины. Весь отрезок, соединяющий две противоположные стороны и перпендикулярный всей из них, дозволено назвать высотой этого четырехугольника. Умение длин сторон, величин углов и высот в различных сочетаниях этих параметров разрешает рассчитать площадь параллелограмма.

Инструкция

1. Если вестима величина угла в всякий вершине параллелограмма (?) и длины прилегающих к нему сторон (a и b), то рассчитать площадь фигуры (S) дозволено с применением тригонометрической функции – синуса. Перемножьте знаменитые длины сторон на синус вестимого угла: S=a*b*sin(?). Скажем, если угол составляет 30°, а длины сторон 15,5 и 8,25 сантиметров, то площадь фигуры будет равна 63,9375 см?, потому что 15,5*8,25*sin(30°)=127,875*0,5=63,9375.

2. Если вестимы длины (a) 2-х параллельных сторон (они идентичны по определению) и высота (h), опущенная на всякую из этих сторон (они тоже идентичны), то этих данных довольно для расчета площади (S) такого четырехугольника. Умножьте знаменитую длину стороны на высоту: S=a*h. Скажем, если длина противоположных сторон составляет 12,25 сантиметров, а высота – 5,75 сантиметров, то площадь параллелограмма будет равна 70,07 см?, потому что 12,25*5,75=70,07.

3. Если длины сторон незнакомы, но есть данные о длинах диагоналей параллелограмма (e и f) и величина угла между ними (?), то этих параметров довольно для вычисления площади (S) фигуры. Обнаружьте половину от произведения вестимых длин диагоналей на синус угла между ними: S=?*e*f*sin(?). Скажем, если длины диагоналей равны 20,25 и 15,75 сантиметрам, а угол между ними равен 25°, то площадь многоугольника составляет примерно 134,7888 см?, потому что 20,25*15,75*sin(25°)?318,9375*0,42261?134,7888.

4. Используйте при расчетах, скажем, калькулятор, совмещенный с функцией поиска в поисковой системе Nigma. Он комфортен тем, что дозволяет рассчитывать площадь параллелограмма, вводя всю последовательности математических действий одной строкой. Скажем, для вычисления площади с данными, приведенными в последнем шаге, введите в строку поискового запроса 20,25*15,75*sin(25) и нажмите кнопку отправки данных на сервер. Сервер вернет рассчитанное значение площади с точностью до 12 знаков позже запятой (134,788811853924).

Видео по теме

Совет 6: Как возвести сечение цилиндра

Линия пересечения поверхности с плоскостью принадлежит единовременно поверхности и секущей плоскости. Линия пересечения цилиндрической поверхности секущей плоскостью, параллельной прямой образующей – прямая линия. Если секущая плоскость перпендикулярна к оси поверхности вращения – в сечении будет окружность. В всеобщем случае линия пересечения цилиндрической поверхности с секущей плоскостью – кривая линия.



Вам понадобится

• Карандаш, линейка, треугольник, лекала, циркуль, измеритель.

Инструкция

1. Пример: возвести сечение цилиндра фронтально-проектирующей плоскостью ?(?₂). В данном примере линия сечения строится по точкам пересечения образующих цилиндра с секущей плоскостью ?.



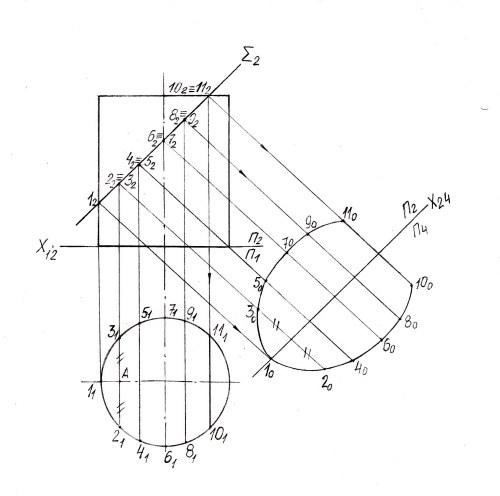
2. На общей плоскости проекций П₂ линия сечения совпадает с проекцией секущей плоскости ?₂ в виде прямой.Обозначьте точки пересечения образующих цилиндра с проекцией ?₂ 1₂, 2₂ и т.д. до точек 10₂ и 11₂.

3. На плоскости П₁ проекция цилиндра – это окружность. Подмеченные на плоскости сечения ?₂ точки 1₂ , 2₂ и т.д. с подмогой линии проекционной связи спроектируются на наброске этой окружности. Обозначьте их горизонтальные проекции симметрично касательно горизонтальной оси окружности.

4. Таким образом, проекции желанного сечения определены: на плоскости П₂ – прямая (точки 1₂, 2₂…10₂); на плоскости П₁ – окружность (точки 1₁, 2₁…10₁).

5. По двум проекциям постройте естественную величину сечения данного цилиндра фронтально-проектирующей плоскостью ?. Для этого используйте метод замены плоскостей проекций.Проведите новую плоскость П₄ параллельно проекции плоскости ?₂. На этой новой оси x₂₄ подметьте точку 1₀. Расстояния между точками 1₂ – 2₂, 2₂ – 4₂ и т.д. с общей проекции сечения отложите на оси x₂₄, проведите тонкие линии проекционной связи перпендикулярно оси x₂₄.В данном методе плоскостью П₄ заменяется плоскость П₁, следственно с горизонтальной проекции размеры от оси до точек перенесите на ось плоскости П₄.

6. Скажем, на П₁ для точек 2 и 3 это будет расстояние от 2₁ и 3₁ до оси(точка А) и т.д.

7. При построении сечения нужно особенно подмечать расположение так называемых опорных точек. К ним относятся точки, лежащие на силуэте проекции (точки 1, 10, 11), на проекции крайних образующих поверхности (точки 6 и 7), точки видимости и т.д.

8. Отложив с горизонтальной проекции указанные расстояния, получите точки 2₀, 3₀, 6₀, 7₀, 10₀, 11₀. После этого для большей точности построения, определяются остальные, промежуточные, точки.

9. Объединив лекальной косой все точки, получите желанную естественную величину сечения цилиндра фронтально-проектирующей плоскостью.

Совет 7: Как определить сечение кабеля по диаметру

Как водится, всякий кабель состоит из нескольких жил, которые в сечении представляют тобой круг. Именно от площади этого сечения пропорционально зависит проводимость кабеля. Если оно будет слишком маленьким, кабель может перегореть, а это одна из основных причин пожаров в современном мире.



Вам понадобится

• – кабель с неведомым сечением;
• – штангенциркуль либо микрометр;
• – таблица удельных сопротивлений веществ.

Инструкция

1. Возьмите кабель, сечение которого надобно определить. Почаще каждого он состоит из 2-4 жил, которые изолированы друг от друга особыми материалами. Эти жилы имеют идентичный диаметр. Изредка дозволено встретить кабель, одна жила которого тоньше остальных – она предуготовлена для заземления.

2. Очистите от изоляции жилы кабеля. С поддержкой штангенциркуля, а отличнее микрометра (это дозволит произвести больше точное измерение), обнаружьте диаметр жилы. Значение получите в миллиметрах. После этого высчитайте площадь поперечного сечения. Для этого показатель 0,25 умножьте на число ??3,14 и значение диаметра d возведенное в квадрат S=0,25???d?. Это значение умножьте на число жил кабеля. Зная длину провода, его сечение и материал из которого он сделан, вычислите его сопротивление.

3. Скажем, если необходимо обнаружить сечение медного кабеля из 4 жил, а измерение диаметра жилы дало значение 2 мм, обнаружьте площадь его поперечного сечения. Для этого рассчитайте площадь поперечного сечения одной жилы. Она будет равна S=0,25?3,14?2?=3,14 мм?. После этого определите сечение каждого кабеля для этого сечение одной жилы умножьте на их число в нашем примере это 3,14?4=12,56 мм?.

4. Сейчас дозволено узнать наивысший ток, тот, что может по нему происходить, либо его сопротивления, если знаменита длина. Наивысший ток для медного кабеля рассчитайте из соотношения 8 А на 1 мм?. Тогда предельное значение тока, тот, что может проходить по кабелю, взятому в примере составляет 8?12,56=100,5 А. Рассматривайте, что для алюминиевого кабеля это соотношение составляет 5 А на 1 мм?.

5. Скажем, длина кабеля составляет 200 м. Для того дабы обнаружить его сопротивление, умножьте удельное сопротивление меди ? в Ом? мм?/м, на длину кабеля l и поделите на площадь его поперечного сечения S (R=??l/S). Сделав подстановку, получите R=0,0175?200/12,56?0,279 Ом, что приведет к дюже малым потерям электроэнергии при ее передаче по такому кабелю.

Совет 8: Как вычислить предел последовательности

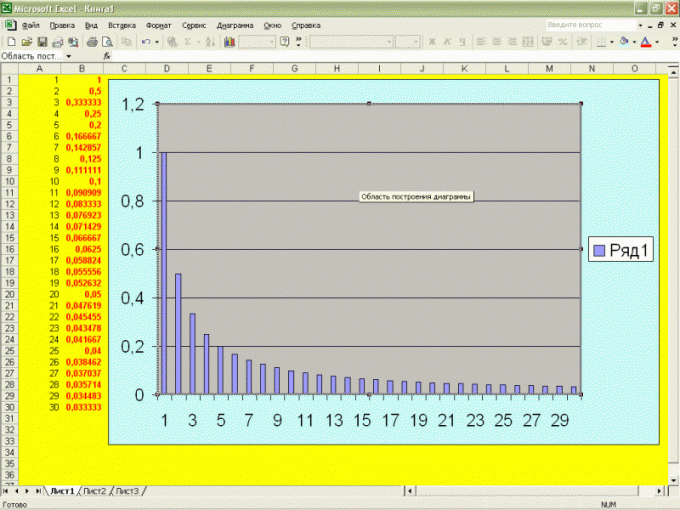
Если переменная, последовательность либо функция имеет безграничное число значений, которые изменяются по некоторому закону, она может тяготиться к определенному числу, которое и является пределом последовательности . Вычислять пределы дозволено разными методами.



Вам понадобится

• – представление числовой последовательности и функции;
• – знание брать производные;
• – знание преобразовывать и уменьшать выражения;
• – калькулятор.

Инструкция

1. Дабы вычислить предел, подставьте в его выражение предельное значение довода. Испробуйте произвести вычисление. Если это допустимо, то значение выражения с подставленным значением и есть желанное число. Пример: Обнаружьте значения предела последовательности с всеобщим членом (3•x?-2)/(2•x?+7), если x > 3. Произведите подстановку предела в выражение последовательности (3•3?-2)/(2•3?+7)=(27-2)/(18+7)=1.

2. Если при попытке подстановки есть неясность, выберите метод, которым ее дозволено устранить. Это дозволено сделать, преобразовав выражения, в которых записывается последовательность. Произведя сокращения, получите итог. Пример: Последовательность (x+vx)/(x-vx), когда x > 0. При прямой подстановке получается неясность 0/0. Избавьтесь от нее, перенесши из числителя и знаменателя всеобщий множитель. В данном случае это будет vx. Получите (vx•(vx+1))/(vx•(vx-1))= (vx+1)/(vx-1). Сейчас поле подстановки получите 1/(-1)=-1.

3. Когда при неопределенности дробь немыслимо сократить (исключительно, если последовательность содержит иррациональные выражения) умножьте ее числитель и знаменатель на спряженное выражение, для того, дабы убрать иррациональность из знаменателя. Пример: Последовательность x/(v(x+1)-1). Значение переменной x > 0. Умножьте числитель и знаменатель на спряженное выражение (v(x+1)+1). Получите (x• (v(x+1)+1))/( (v(x+1)-1)•(v(x+1)+1))=(x• (v(x+1)+1))/(x+1-1)= (x• (v(x+1)+1))/x=v(x+1)+1. Произведя подстановку, получите =v(0+1)+1=1+1=2.

4. При неопределенностях типа 0/0 либо ?/? используйте правило Лопиталя. Для этого числитель и знаменатель последовательности представьте как функции, возьмите из них производные. Предел их отношений будет равен пределу отношений самих функций. Пример: Обнаружить предел последовательности ln(x)/vx, при x > ?. Прямая подстановка дает неясность ?/?. Возьмите производные из числителя и знаменателя и получите (1/x)/(1/2•vx)=2/vx=0.

5. Для раскрытия неопределенностей пользуйтесь первым восхитительным пределом sin(x)/x=1 при x>0, либо вторым восхитительным пределом (1+1/x)^x=exp при x>?. Пример: Обнаружить предел последовательности sin(5•x)/(3•x) при x>0. Преобразуйте выражение sin(5•x)/(3/5•5•x) вынесите множитель из знаменателя 5/3•( sin(5•x)/(5•x)) применяя 1-й восхитительный предел получите 5/3•1=5/3.

6. Пример: Обнаружить предел (1+1/(5•x))^(6•x) при x>?. Умножьте и поделите показатель степени на 5•x. Получите выражение ((1+1/(5•x))^(5•x)) ^(6•x)/(5•x). Применив правило второго восхитительного предела, получите exp^(6•x)/(5•x)=exp.

Видео по теме

Совет 9: Как обнаружить площадь осевого сечения усеченного конуса

Дабы решить данную задачу, нужно припомнить, что такое усеченный конус и какими свойствами он владеет. Непременно сделайте чертеж. Это дозволит определить, какую геометрическую фигуру представляет собой сечение конуса . Абсолютно допустимо, что позже этого решение задачи теснее не будет представлять для вас трудности.

Инструкция

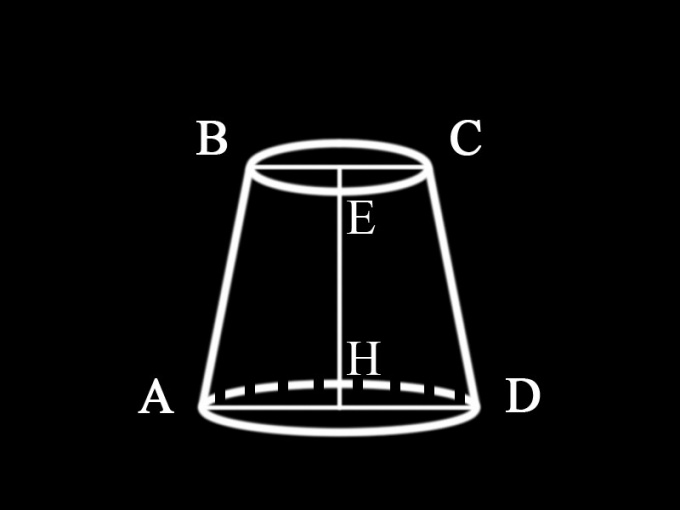
1. Круглый конус – тело, полученное путем вращения треугольника вокруг одного из его катетов. Прямые, исходящие из вершины конуса и пересекающие его основание, именуются образующими. Если все образующие равны, то конус является прямым. В основании круглого конуса лежит круг. Перпендикуляр, опущенный на основание из вершины, является высотой конуса . У круглого прямого конуса высота совпадает с его осью. Ось – это прямая, соединяющая вершину с центром основания. Если горизонтальная секущая плоскость кругового конуса параллельна основанию, то его верхнее основание представляет собой круг.

2. От того что в условии задачи не оговорено, какой именно конус дается в данном случае, дозволено сделать итог, что это круглый прямой усеченный конус, горизонтальное сечение которого параллельно основанию. Его осевое сечение, т.е. вертикальная плоскость, которая проходит через ось круглого усеченного конуса , представляет собой равнобочную трапецию. Все осевые сечения круглого прямого конуса равны между собой. Следственно, дабы обнаружить площадь осевого сечения , требуется обнаружить площадь трапеции, основаниями которой являются диаметры оснований усеченного конуса , а боковые стороны – его образующие. Высота усеченного конуса является единовременно высотой трапеции.

3. Площадь трапеции определяется по формуле:S = ?(a+b) h, где S – площадь трапеции;a – величина нижнего основания трапеции;b – величина ее верхнего основания;h – высота трапеции.

4. От того что в условии не оговорено, какие именно величины даны, дозволено считать, что диаметры обеих оснований и высота усеченного конуса знамениты: AD = d1 – диаметр нижнего основания усеченного конуса ;BC = d2 – диаметр его верхнего основания; EH = h1 – высота конуса .Таким образом, площадь осевого сечения усеченного конуса определяется: S1 = ? (d1+d2) h1

Совет 10: Как перевести сечение в диаметр

В нормативных документах по проектированию электросетей указывают сечения проводов, а штангенциркулем дозволено измерить только диаметр жилы. Величины эти взаимосвязаны и могут быть переведены одна в иную.

Инструкция

1. Дабы перевести указанное в нормативном документе сечение одножильного провода в его диаметр, воспользуйтесь дальнейшей формулой:D=2sqrt(S/?), где D – диаметр, мм; S – сечение проводника, мм2 (именно квадратные миллиметры электрики сокращенно называют «квадратами»).

2. Эластичный многожильный провод состоит из множества тонких жил, скрученных между собой и размещенных в всеобщую изоляционную оболочку. Это разрешает ему не ломаться при частых перемещениях нагрузки, которая подключена при его помощи к источнику питания. Дабы обнаружить диаметр одной жилы такого проводника (именно ее дозволено измерить штангенциркулем), сначала обнаружьте сечение этой жилы:s=S/n, где s – сечение одной жилы, мм2; S – суммарное сечение провода (указывается в нормативных документах); n – число жил.После этого переведите сечение жилы в диаметр, как указано выше.

3. На печатных платах применяются плоские проводники. Взамен диаметра они имеют толщину и ширину. Первая величина знаменита заблаговременно из технических данных фольгированного материала. Зная ее, дозволено обнаружить ширину по сечению. Для этого используйте такую формулу:W=S/h, где W – ширина проводника, мм; S – сечение проводника, мм2; h – толщина проводника, мм.

4. Проводники квадратного сечения встречаются относительно редко. Его сечение подлежит переводу либо в длину стороны, либо в диагональ квадрата (штангенциркулем дозволено измерить и то, и другое). Длина стороны вычисляется дальнейшим образом:L=sqrt(S), где L – длина стороны, мм; S – сечение проводника, мм2.Дабы после этого по длине стороны узнать диагональ, произведите следующие вычисления:d=sqrt(2(L^2)), где d – диагональ квадрата, мм; L – длина стороны, мм.

5. Если проводника, сечение которого верно соответствует требуемому, не окажется, используйте иной, имеющий большее, но ни в коем случае не меньшее сечение. Тип проводника и вид его изоляции выбирайте в зависимости от условий использования.

Обратите внимание!
Перед измерением проводника штангенциркулем снимите питающее напряжение и удостоверитесь в его отсутствии при помощи вольтметра.

Совет 11: Как вычислить площадь окружности

Вычислить площадь окружности немыслимо, чай это линия, представление площади для нее не определено. Но дозволено вычислить площадь круга, ограниченного этой окружностью. Для решения задачи нужно знать радиус.

Инструкция

1. Кругом радиуса R является такое геометрическое место точек плоскости, что расстояние от центра круга до них не превышает радиуса. Граница круга – окружность – геометрическое место точек, расстояние от которых до центра равно радиусу R.

2. Площадь – колляция плоской фигуры. Условно дозволено сказать, что она показывает, сколько места занимает фигура на плоскости. В всеобщем случае, площадь находится путем взятия определенного интеграла от функции y(x).

3. Если вестим радиус круга, обнаружьте его площадь по формуле S=?•R?, где S – площадь , ? – число «пи», R – радиус. Число «пи» – трансцендентное иррациональное число, константа, равная приблизительно 3,14. Она выражает отношение длины окружности к длине диаметра: ?=L/D=L/2R.

4. Пример. Окружность имеет радиус 2 см. Вычислите площадь круга, ограниченного этой окружностью.Решение. Если применить формулу для нахождения площади круга через радиус, то S=?•R?=?•2?=4??3,14•2??12,56 (см?). Изредка число ? не подставляют, оставляя результат в виде S=4?. Такой результат менее наглядный (сложно представить число «пи»), но математически больше точный.

5. Если теснее знаменита длина окружности , дозволено считать площадь круга через нее: S=L•R/2. Кстати, длина окружности выражается через радиус формулой L=2•? •R.

6. Возведя в круге центральный угол, дозволено получить сектор. Сектором называют часть круга, ограниченную дугой и двумя радиусами, которые соединяют центр круга с концами этой дуги. Дабы обнаружить площадь сектора, нужно знать не только радиус, но и угол ?: S(сектора)=?•R?/2. Тут ? – угол в радианах. Длина дуги определяется соотношением L(дуги)=?•R.

7. В комплексном обзоре существует такое идиоматическое представление, как единичный круг – круг радиуса 1. Его площадь , соответственно, равна S=?.

Видео по теме

Совет 12: Как вычислить площадь цилиндра

Цилиндр является пространственной фигурой и состоит из 2-х равных оснований, которые представляют собой круги и боковой поверхности, соединяющей линии, ограничивающие основания. Дабы вычислить площадь цилиндра , обнаружьте площади всех его поверхностей и сложите их.



Вам понадобится

• линейка;
• калькулятор;
• понятие площади круга и длины окружности.

Инструкция

1. Определите площадь оснований цилиндра . Для этого измерьте при помощи линейки диаметр основания, после этого поделите его на 2. Это будет радиус основания цилиндра . Вычислите площадь одного основания. Для этого возведите значение его радиуса в квадрат и умножьте на непрерывную ?, Sкр= ??R?, где R – радиус цилиндра , а ??3,14.

2. Обнаружьте всеобщую площадь 2-х оснований, исходя из определения цилиндра , которое говорит о том, что его основания равны между собой. Площадь одного круга основания умножьте на 2, Sосн=2?Sкр=2???R?.

3. Вычислите площадь боковой поверхности цилиндра . Для этого обнаружьте длину окружности, которая ограничивает одно из оснований цилиндра . Если радиус теснее вестим, то вычислите ее, умножив число 2 на ? и радиус основания R, l= 2???R, где l – длина окружности основания.

4. Измерьте длину образующей цилиндра , которая равна длине отрезка, соединяющего соответствующие точки основания либо их центры. В обыкновенном прямом цилиндре образующая L численно равна его высоте H. Рассчитайте площадь боковой поверхности цилиндра , умножив длину его основания на образующую Sбок= 2???R?L.

5. Вычислите площадь поверхности цилиндра , суммировав площадь оснований и боковой поверхности. S=Sосн+ Sбок. Подставив формульные значения поверхностей, получите S=2???R?+2???R?L, вынесите всеобщие множители S=2???R?(R+L). Это дозволит рассчитать поверхность цилиндра при помощи цельной формулы.

6. Скажем, диаметр основания прямого цилиндра составляет 8 см, а его высота равна 10 см. Определите площадь его боковой поверхности. Вычислите радиус цилиндра . Он равен R=8/2=4 см. Образующая прямого цилиндра равна его высоте, то есть L=10 см. Для расчетов используйте цельную формулу, это комфортнее. Тогда S=2???R?(R+L), подставьте соответствующие числовые значения S=2?3,14?4?(4+10)=351,68 см?.

Видео по теме

Совет 13: Как определить площадь поперечного сечения

Если поперечное сечение объекта имеет трудную форму, для вычисления его площади следует разбить его на участки примитивных форм. Позже этого появится вероятность рассчитать площади этих участков по соответствующим формулам, а после этого их сложить.

Инструкция

1. Поделите поперечное сечение объекта на области, имеющие формы треугольников, прямоугольников, квадратов, секторов, кругов, полукругов и четвертей кругов. Если в итоге распределения будут получаться ромбы, поделите весь из них на два треугольника, а если параллелограммы – на два треугольника и один прямоугольник. Измерьте размеры всей из этих областей: стороны, радиусы. Все измерения осуществляйте в идентичных единицах.

2. Прямоугольный треугольник дозволено представить в виде половины прямоугольника, поделенного надвое по диагонали. Для расчета площади такого треугольника умножьте друг на друга длины тех сторон, которые примыкают к прямому углу (они именуются катетами), после этого итог умножения поделите на два. Если же треугольник прямоугольным не является, для расчета его площади сначала проведите в нем из всякого угла высоту. Он окажется поделенным на два различных треугольника, всякий из которых будет прямоугольным. Измерьте длины катетов всего из них, а после этого по итогам измерений вычислите их площади.

3. Дабы вычислить площадь прямоугольника, умножьте друг на друга длины 2-х его примыкающих друг к другу сторон. У квадрата они равны, следственно дозволено длину одной стороны умножить саму на себя, то есть, построить ее в квадрат.

4. Для определения площади круга поделите возведите его радиус в квадрат, а после этого умножьте итог на число ?. В случае, если фигура является не кругом, а полукругом, поделите площадь на два, а если четвертью круга – на четыре. У сектора измерьте угол между центром воображаемого центра и концами дуги, переведите его из градусов в радианы, умножьте на квадрат радиуса, а после этого поделите на два.

5. Сложите все полученные площади между собой, и получится площадь , выраженная в единицах того же порядка, что и начальные данные. Скажем, если длины сторон и радиусы измерялись вами в миллиметрах, площадь получится в квадратных миллиметрах.

6. Гораздо облегчить измерение площади трудной фигуры поможет прибор, называемый планиметром. Установите его шкалу на нуль, позже чего проведите щупом по силуэту фигуры. Прочитайте показания шкалы. Точность такого измерения получится относительно маленький.

Видео по теме

Совет 14: Как вычислить площадь фигуры, ограниченной параболой

Еще из школьного курса знаменито, что для нахождения площадей фигур на координатной плоскости нужно умение такого представления, как интеграл. Для его использования в целях определения площадей криволинейных трапеций – именно так и именуются эти фигуры – довольно знать определенные алгорифмы.

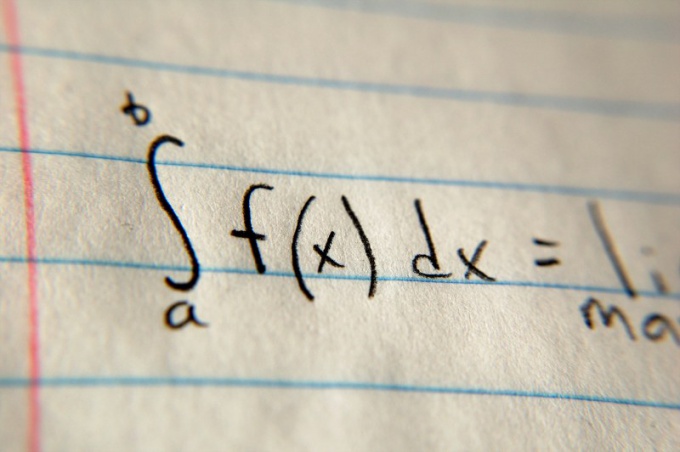
Инструкция

1. Дабы вычислить площадь фигуры, ограниченной параболой, изобразите ее в декартовой системе координат. Для изображения параболы следует знать минимум три точки, одна должна быть вершиной. Дабы обнаружить координату вершины по оси X, подставьте вестимые данные в формулу x=-b/2a, по оси Y подставьте полученное значение довода в функцию. Позже этого проанализируйте данные графика, входящие в условие задачи. Если вершина ниже оси Х, то ветви будут направлены вверх, если выше — вниз. Остальные 2 точки — это координаты пересечения с осью ОХ. Заштрихуйте полученную фигуру. Это значительно облегчит решение данной задачи.

2. Позже этого определите пределы интегрирования. Обыкновенно они указаны в условии задачи с подмогой переменных a и b. Эти значения разместите в верней и нижней частях символа интеграла соответственно. Позже символа интеграла впишите значение функции в всеобщем виде и помножьте его на dx (скажем, (x²)dx в случае с параболой). После этого вычислите первообразную значения функции в всеобщем виде, воспользовавшись особой таблицей по ссылке, приведенной в разделе «Добавочные источники», позже чего подставьте туда пределы интегрирования и обнаружьте разность. Полученная разность и будет площадью.

3. Также существует вероятность вычисления интеграла и программным способом. Для этого перейдите по ссылке, находящейся в разделе «Добавочные источники», на особый математический сайт. В открывшееся текстовое поле введите integral of f(x), где f(x) — запись функции, график которой ограничивает площадь фигуры на координатной плоскости. Позже ввода нажмите на кнопку в виде символа «равно». Открывшаяся страница изобразит полученную фигуру, а также покажет ход вычислений ее площади.

Совет 15: Как обнаружить площадь сечения куба

Вопрос относится к аналитической геометрии. Он решается с привлечением уравнений пространственных прямых и плоскостей, представления куба и его геометрических свойств, а также с применением векторной алгебры. Могут потребоваться методы рения систем линейных уравнений.

Инструкция

1. Выберите данные задачи так, дабы они были исчерпывающими, но не избыточными. Секущую плоскость ? следует задать всеобщим уравнением вида Ax+By+Cz+D=0, что наилучшим образом согласуется с произвольным его выбором. Для задания куба абсолютно хватит координат всяких 3 его вершин. Возьмите, скажем, точки M1(x1,y1,z1), M2(x2,y2,z2), M3(x3,y3,z3), в соответствии с рисунком 1. На этом рисунке проиллюстрировано сечение куба. Оно пересекает два боковых ребра и три ребра оснований.



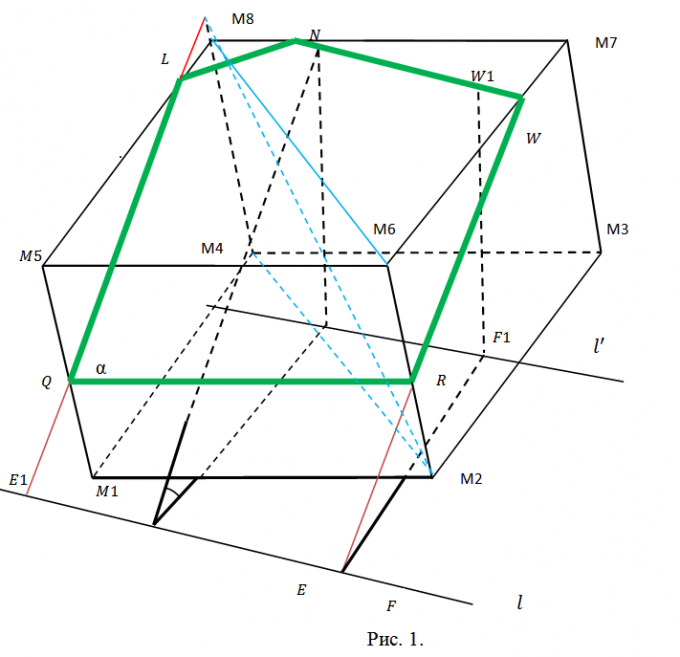
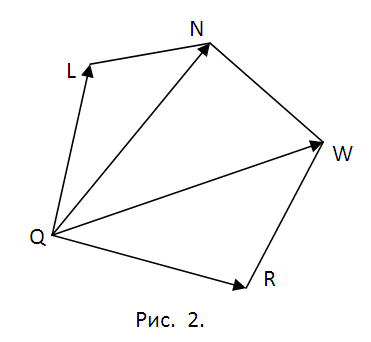
2. Определитесь с планом последующей работы. Предстоит искать координаты точек Q, L, N, W, R пересечения сечения с соответствующими ребрами куба. Для этого придется находить уравнения прямых, содержащих эти ребра, и искать точки пересечения ребер с плоскостью ?. Позже этого последует разбиение пятиугольника QLNWR на треугольники (см. рис. 2) и вычисление пощади всего из них с подмогой свойств векторного произведения. Методология всякий раз одна и та же. Следственно дозволено ограничиться точками Q и L и площадью треугольника ?QLN.



3. Направляющий вектор h прямой, содержащий ребро М1М5 (и точку Q), обнаружьте как векторное произведение M1M2={x2-x1, y2-y1, z2-z1} и M2M3={x3-x2, y3-y2, z3-z2}, h={m1, n1, p1}=[M1M2? M2M3]. Полученный вектор является направляющим и для всех прочих боковых ребер. Длину ребра куба обнаружьте как, скажем, ?=?( (x2-x1)^2+(y2-y1)^2+(z2-z1)^2). Если модуль вектора h |h|??, то замените его соответствующим коллинеарным вектором s={m, n, p}=(h/|h|)?. Сейчас запишите уравнение прямой, содержащей М1М5 параметрически (см. рис. 3). Позже подстановки соответствующих выражений в уравнение секущей плоскости получите А(x1+mt)+B(y1+nt)+C(z1+pt)+D=0. Определите t, подставьте в уравнения для М1М5 и запишите координаты точки Q(qx, qy, qz) (рис. 3).



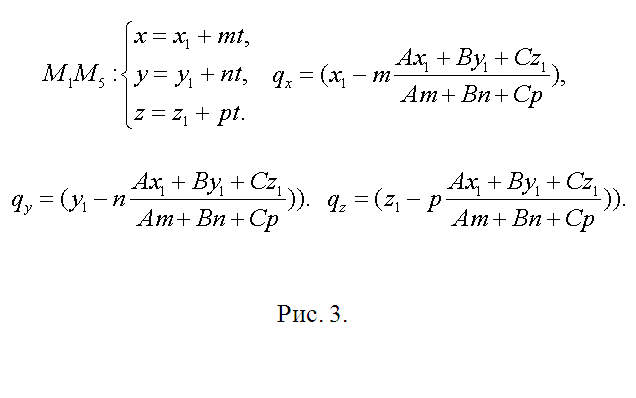
4. Видимо, что точка М5 имеет координаты М5(x1+m, y1+n, z1+p). Направляющий вектор для прямой, содержащей ребро М5М8 совпадает с М2М3={x3-x2, y3-y2,z3-z2}. После этого повторите предыдущие рассуждения касательно точки L(lx, ly, lz) (см. рис. 4). Все последующее, для N(nx, ny, nz) – точная копия это шага.



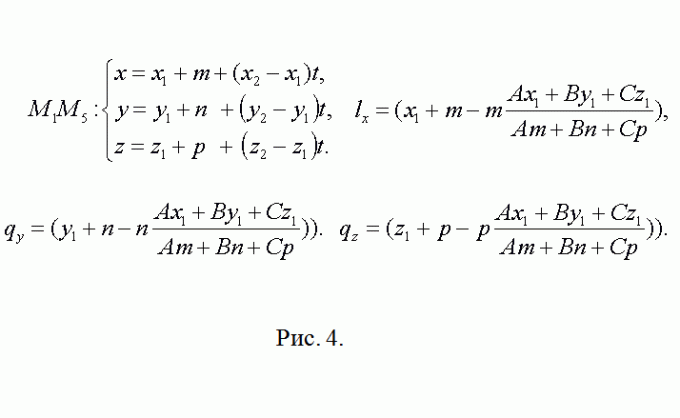
5. Запишите векторы QL={lx-qx, ly-qy, lz-qz} и QN={nx-qx, ny-qy, nz-qz}. Геометрический толк их векторного произведения состоит в том, что его модуль равен площади параллелограмма построенного на векторах. Следственно площадь ?QLN S1=(1/2)|[QL? QN]|. Следуйте предложенной методике и вычислите площади треугольников ?QNW и ?QWR – S1 и S2. Векторное произведение комфортнее каждого находить с поддержкой вектора-определителя (см. рис. 5). Запишите окончательный результат S=S1+S2+S3.



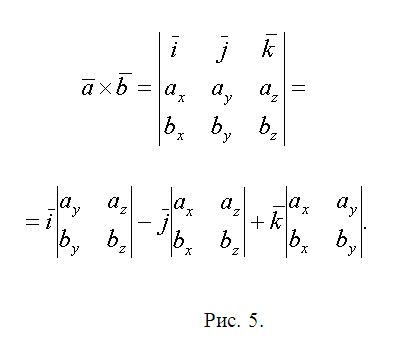
Обратите внимание!
Двукратно пересчитывайте полученный итог: так вы не допустите ошибки в расчетах.

Полезный совет
Дабы рассчитать площадь сечения всякий иной геометрической фигуры, воспользуйтесь математическим справочником, в котором подобраны формулы для расчета и даны подробные рекомендации.