Совет 1: Как построить трехчлен в квадрат

Многочлен – алгебраическая конструкция, представляющая собой сумму либо разность элементов. Множество готовых формул касается двучленов, впрочем вывести новые для конструкций больше высокого порядка не составляет большого труда. Дозволено, скажем, построить трехчлен в квадрат .

Инструкция

1. Многочлен является основным представлением для решения алгебраических уравнений и представления степенной, разумной и прочих функций. К этой структуре относится особенно распространенное в школьном курсе предмета квадрат ное уравнение.

2. Зачастую по мере облегчения массивного выражения появляется надобность построить трехчлен в квадрат . Для этого нет готовой формулы, впрочем есть несколько способов. Скажем, представить квадрат трехчлен а в виде произведения 2-х идентичных выражений.

3. Разглядите пример: возведите в квадрат трехчлен 3•х? + 4•х – 8.

4. Измените запись (3•х? + 4•х – 8)? на (3•х? + 4•х – 8)•( 3•х? + 4•х – и воспользуйтесь правилом умножения многочленов, которое состоит в последовательном вычислении произведений. Вначале умножьте первое составляющее первой скобки на всякое слагаемое 2-й, после этого так же поступите со вторым и, наконец, с третьим:(3•х? + 4•х – 8)•( 3•х? + 4•х – = 3•х?•(3•х? + 4•х – + 4•х•(3•х? + 4•х – – 8•(3•х? + 4•х – = 9•х^4 + 12•х? – 24•х? + 12•х? + 16•х? – 32•х – 24•х? – 32•х + 64 = 9•х^4 + 24•х? – 32•х? – 64•х + 64.

5. К тому же итогу дозволено придти, если запомнить, что в итоге перемножения 2-х трехчлен ов остается сумма из шести элементов, три из которых являются квадрат ами всякого слагаемого, а три остальных – их всевозможными попарными произведениями в удвоенной форме. Эта элементарная формула элементарно выглядит так:(a + b + c)? = a? + b? + c? + 2•a•b + 2•a•c + 2•b•c.

6. Примените ее к вашему примеру:(3•х? + 4•х – 8)? = (3•х? + 4•х + (-8))? =(3•х?)? + (4•х)? + (-8)? + 2•(3•х?)•(4•х) + 2•(3•х?)•(-8) + 2•(4•х)•(-8) = 9•х^4 + 16•х? + 64 + 24•х? – 48•х? – 64•х = 9•х^4 + 24•х? – 32•х? – 64•х + 64.

7. Как видите, результат получился тот же, а манипуляций понадобилось поменьше. Это исключительно главно, когда одночлены сами по себе являются трудными конструкциями. Данный метод применим для трехчлен а всякий степени и всякого числа переменных.

Совет 2: Как построить дробь в квадрат

При решении арифметических и алгебраических задач изредка требуется построить дробь в квадрат . Проще каждого это сделать, когда дробь десятичная – довольно обыкновенного калькулятора. Впрочем если дробь обычная либо смешанная, то при возведении такого числа в квадрат могут появиться некоторые затруднения.



Вам понадобится

• калькулятор, компьютер, приложение Excel.

Инструкция

1. Дабы построить десятичную дробь в квадрат , возьмите инженерный калькулятор, наберите на нем возводимую в квадрат дробь и нажмите на клавишу возведения во вторую степень. На большинстве калькуляторов эта кнопка обозначена как «х?». На стандартном калькуляторе Windows функция возведения в квадрат выглядит как «x^2». Скажем, квадрат десятичной дроби 3,14 будет равен: 3,14? = 9,8596.

2. Дабы построить в квадрат десятичную дробь на обыкновенном (бухгалтерском) калькуляторе, умножьте это число само на себя. Кстати, в некоторых моделях калькуляторов предусмотрена вероятность возведения числа в квадрат даже при отсутствии особой кнопки. Следственно заблаговременно ознакомьтесь с инструкцией к определенному калькулятору. Изредка примеры «хитроумного» возведения в степень приведены на задней крышке либо на коробке калькулятора. Скажем, на многих калькуляторах для возведения числа в квадрат довольно нажать кнопки «х» и «=».

3. Для возведения в квадрат обычной дроби (состоящей из числителя и знаменателя), возведите в квадрат по отдельности числитель и знаменатель этой дроби. То есть воспользуйтесь дальнейшим правилом:(ч / з)? = ч? / з?, где ч – числитель дроби, з – знаменатель дроби.Пример: (3/4)? = 3?/4? = 9/16.

4. Если возводимая в квадрат дробь – смешанная (состоит из целой части и обычной дроби), то заблаговременно приведите ее к обычному виду. То есть примените следующую формулу:(ц ч/з)? = ((ц*з+ч) / з)? = (ц*з+ч)? / з?, где ц – целая часть смешанной дроби.Пример: (3 2/5)? = ((3*5+2) / 5)? = (3*5+2)? / 5? = 17? / 5? = 289/25 = 11 14/25.

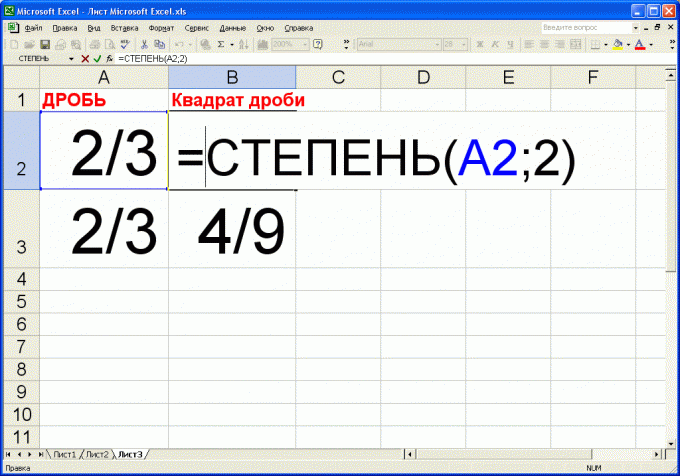
5. Если возводить в квадрат обычные (не десятичные) дроби доводится непрерывно, то воспользуйтесь программой MS Excel. Для этого введите в одну из клеток таблицы следующую формулу: =СТЕПЕНЬ(A2;2) где А2 – адрес ячейки, в которую будет вводиться возводимая в квадрат дробь .Дабы осведомить программе, что с вводимым числом нужно обращаться как с обычной дробь ю (т.е. не преобразовывать ее в десятичный вид), наберите перед дробь ю цифру «0» и знак «пробел». То есть для ввода, скажем, дроби 2/3 необходимо ввести: «0 2/3» (и нажать Enter). При этом в строке ввода отобразится десятичное представление введенной дроби. Значение и представление дроби непринужденно в клетке сохранится в начальном виде. Помимо того, при применении математических функций, доводами которых являются обычные дроби, итог также будет представлен в виде обычной дроби. Следственно квадрат дроби 2/3 будет представлен как 4/9.

Совет 3: Как составить волшебный квадрат

Математические головоломки изредка увлекают так, что хочется обучиться создавать их, а не только решать. Вероятно, самым увлекательным для новичков является создание магического квадрата, тот, что представляет собой квадрат с размерами сторон nxn, в тот, что вписаны настоящие числа от 1 до n2 так, что сумма чисел по горизонталям, вертикалям и диагоналям квадрата является идентичной и равняется одному числу.

Инструкция

1. Раньше чем составлять свой квадрат, усвойте, что магических квадратов второго порядка не бывает. Волшебный квадрат третьего порядка существует реально только один, остальные производные от него получаются с подмогой поворота либо отражения основного квадрата по оси симметрии. Чем огромнее порядок, тем огромнее существует допустимых волшебных квадратов этого порядка.

2. Изучите основы построения. Правила построения различных магических квадратов подразделяются на три группы по порядку квадрата, а именно он может быть нечетным, равным удвоенному либо учетверенному нечетному числу. Всеобщей методологии для построения всех квадратов в текущее время не существует, правда обширно распространены различные схемы.

3. Воспользуйтесь компьютерной программой. Скачайте надобное приложение и введите желаемые значения квадрата (2-3), программа сама генерирует надобные цифровые комбинации.

4. Постройте квадрат независимо. Возьмите матрицу n x n , внутри которой произведите построение ступенчатого ромба. В нем заполните все квадратики слева и вверх по каждым диагоналям последовательностью нечетных чисел.

5. Определите значение центральной ячейки О. В углах магического квадрата расположите такие числа: верхняя правая ячейка – О-1, нижняя левая – О+1, правая внизу – О-n, а левая вверху – О+n. Пустые ячейки в угловых треугольниках заполните, применяя довольно примитивные правила: в строках по направлению слева направо числа возрастают на n + 1, а в столбиках по направлению сверху вниз числа возрастают на n-1.

6. Найти все квадраты с порядком равным n получается только для n\le 4, следственно увлекательны отдельные процедуры для построения магических квадратов с n > 4. Проще каждого рассчитать проектирование такого квадрата нечетного порядка. Воспользуйтесь особой формулой, куда требуется примитивно поставить нужные данные для приобретения желаемого итога. Скажем, константа квадрата, построенного по схеме с рис. 1, вычисляется по формуле: S = 6a1 +105b, где a1 – 1-й член прогрессии, b – разность прогрессии.



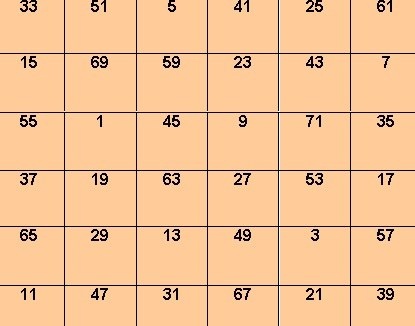
7. Для квадрата, изображенного на рис. 2, формула: S = 6*1 + 105*2 = 216



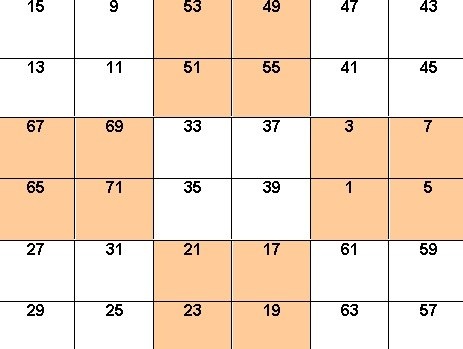
8. Помимо этого, существуют алгорифмы для построения пандиагональных квадратов и совершенных магических квадратов. Воспользуйтесь особыми программами построения этих моделей.

Обратите внимание!
Волшебные, либо магические, квадраты привлекали математиков с самых древних времен, но изложения всех допустимых квадратов нет и по сей день. Самый легкой волшебный квадрат согласно старинной китайской легенде был изображен на спине крупный священной черепахи.

Совет 4: Как обнаружить квадрат уравнения

«Уравнением» в математике именуется запись, содержащую некоторые математические либо алгебраические действия и непременно включающую в себя знак равенства. Впрочем почаще этим представлением обозначают не тождество в совокупности, а только его левую часть. Следственно задача возведения уравнения в квадрат скорее каждого полагает использование этой операции только к одночлену либо многочлену в левой части равенства.

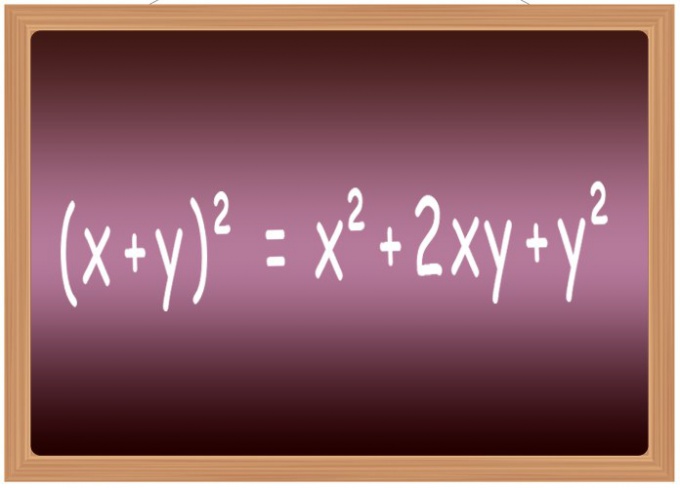
Инструкция

1. Умножьте уравнение на само себя – это и есть операция возведения во вторую степень, то есть в квадрат . Если начальное выражение содержит переменные в какой-нибудь степени, то показатель степени следует увеличить в два раза. Скажем, (4*x?)? = (4*x?)*(4*x?) = 16*x?. Если присутствующие в уравнении численные показатели умножить в уме не представляется допустимым, то используйте калькулятор, онлайн-вычислитель либо сделайте это на бумаге, «в столбик».

2. Если начальное выражение содержит несколько складываемых либо вычитаемых переменных с численными показателями (то есть является многочленом), то придется осуществлять операцию умножения по соответствующим правилам. Это обозначает, что следует перемножить весь член уравнения -множимого на весь член уравнения -множителя, а после этого упростить полученное выражение. Тот факт, что в вашем случае оба уравнения идентичны, ничего не меняет в этом правиле. Скажем, если построить в квадрат требуется уравнение x?+4-3*x, то всю операцию дозволено записать в таком виде: (x?+4-3*x)? = (x?+4-3*x)*(x?+4-3*x) = x?+4*x?-3*x? + 4*x?+16-12*x – 3*x?-12*x+9*x?. Полученное выражение следует упростить и, если это допустимо, расположить степенные члены в порядке убывания показателя степени: x?+4*x?-3*x? + 4*x?+16-12*x – 3*x?-12*x+9*x? = x? – 6*x? + 25*x? – 24*x + 16.

3. Формулы возведения в квадрат некоторых особенно зачастую встречающихся выражений отличнее запомнить назубок. В школе их обыкновенно включают в список, называемый «формулами сокращенного умножения». В него относят, в частности, формулы возведения во вторую степень суммы 2-х переменных (x+y)? = x?+2*x*y+y?, их разности (x-y)? = x?-2*x*y+y?, суммы 3 слагаемых (x+y+z)? = x?+y?+z?+2*x*y+2*y*z+2*x*z и разности 3 слагаемых (x-y-z)? = x?+y?+z?-2*x*y+2*x*y-2*z.

Видео по теме

Совет 5: Как выделить квадрат двучлена

Способ выделения квадрата двучлена используется при облегчении массивных выражений, а также для решения квадратных уравнений. На практике его обыкновенно комбинируют с другими приемами, включая разложение на множители, группировку и пр.

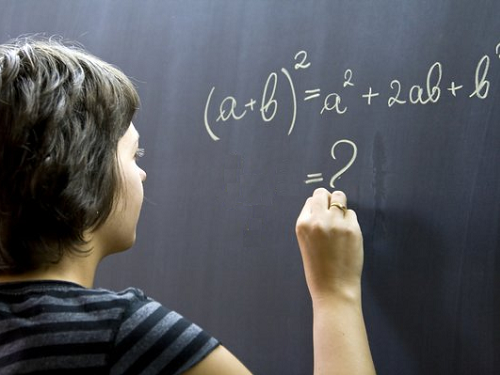
Инструкция

1. Способ выделения полного квадрата двучлена основан на применении 2-х формул сокращенного умножения многочленов. Эти формулы являются частными случаями Бинома Ньютона для 2-й степени и разрешают упростить желанное выражение так, дабы дозволено было провести дальнейшее сокращение либо разложение на множители:(m + n)² = m² + 2·m·n + n²;(m – n)² = m² – 2·m·n + n².

2. Согласно этому способу из начального многочлена требуется выделить квадраты 2-х одночленов и сумму/разность их двойного произведения. Использование этого способа имеет толк, если старшая степень слагаемых не поменьше 2. Представим, дано задание разложить на множители с понижением степени следующее выражение:4·y^4 + z^4

3. Для решения задачи надобно воспользоваться способом выделения полного квадрата. Выходит, выражение состоит из 2-х одночленов с переменными четной степени. Следственно, дозволено обозначить всякий из них через m и n:m = 2·y²; n = z².

4. Сейчас надобно привести начальное выражение к виду (m + n)². В нем теснее присутствуют квадраты этих слагаемых, но не хватает двойного произведения. Надобно добавить его неестественно, а потом вычесть:(2·y²)² + 2·2·y²·z² + (z²)² – 2·2·y² ·z² = (2·y² + z²)² – 4·y²·z².

5. В получившемся выражении дозволено увидеть формулу разности квадратов:(2·y² + z²)² – (2·y·z)² = (2·y² + z² – 2·y·z)· (2·y² + z² + 2·y·z).

6. Выходит, способ состоит из 2-х этапов: выделение одночленов полного квадрата m и n, прибавление и вычитание их двойного произведения. Способ выделения полного квадрата двучлена может использоваться не только самосильно, но и в комбинации с другими способами: вынесения за скобки всеобщего множителя, замена переменной, группировки слагаемых и пр.

7. Пример 2.Выделите полный квадрат в выражении:4·y² + 2·y·z + z².Решение.4·y² + 2·y·z + z² =[m = 2·y, n = z] = (2·y)² + 2·2·y·z + (z) ² – 2·y·z = (2·y + z)² – 2·y·z.

8. Способ используется при нахождении корней квадратного уравнения. Левая часть уравнения представляет собой трехчлен вида a·y? + b·y + c, где a, b и c – какие-то числа, причем a ? 0. a·y? + b·y + c = a·(y? + (b/a)·y) + c = a·(y? + 2·(b/(2·a))·y) + c = a·(y? + 2·(b/(2·a))·y + b?/(4·a?)) + c – b?/(4·a) = a·(y + b/(2·a)) ? – (b? – 4·a·c)/(4·a).

9. Эти расчеты приводят к представлению дискриминанта, тот, что равен (b? – 4·a·c)/(4·a), а корни уравнения равны:y_1,2 = ±(b/(2•a)) ± ? ((b? – 4·a·c)/(4·a)).

Совет 6: Как выделить из трехчлена квадрат двучлена

Есть несколько способов решения квадратного уравнения, особенно общеизвестный – выделить из трехчлена квадрат двучлена. Данный метод приводит к вычислению дискриминанта и обеспечивает одновременный поиск обоих корней.

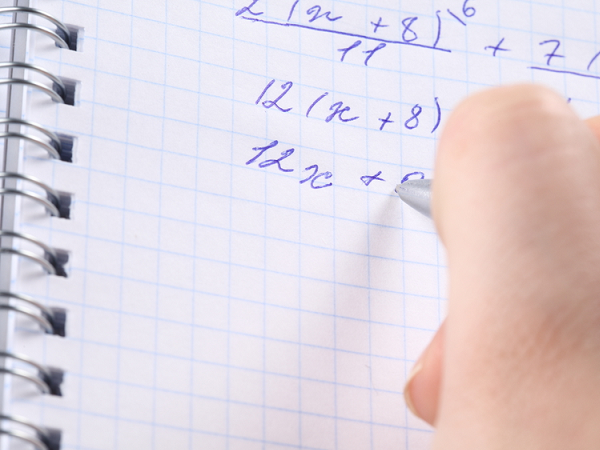
Инструкция

1. Алгебраическое уравнение 2-й степени именуется квадратным. Классическая форма левой стороны этого уравнения представляет собой многочлен a•x? + b•x + c. Дабы вывести формулу для решения, нужно выделить из трехчлена квадрат двучлена. Это дозволено осуществить двумя методами. Перенесите вольный член с в правую сторону со знаком минус:a•x? + b•x = -c.

2. Умножьте обе стороны уравнения на 4•а:4•a?•x? + 4•a•b•x = -4•a•c.

3. Прибавьте выражение b?:4•a?•x? + 4•a•b•x + b? = -4•a•c + b?.

4. Видимо, что слева получилась развернутая форма квадрата двучлена, состоящего из слагаемых 2•a•x и b. Сверните данный трехчлен в полный квадрат:(2•a•x + b)? = b? – 4•a•c ? 2•a•x + b = ±?(b? – 4•a•c)

5. Откуда:x1,2 = (-b ± ?(b? – 4•a•c))/2•a.Разность, стоящая под знаком корня, именуется дискриминантом, а формула является общеизвестной для решения сходственных уравнений.

6. 2-й метод подразумевает выделение из одночлена первой степени удвоенного произведения элементов. Т.е. нужно определить из слагаемого вида b•x, какие множители могут быть использованы для полного квадрата. Данный способ отменнее разглядеть на примере:x? + 4•x + 13 = 0

7. Посмотрите на одночлен 4•x. Видимо, что его дозволено представить в виде 2•(2•x), т.е. удвоенного произведения х и 2. Следственно, выделять надобно квадрат суммы (х + 2). Для полноты картины не хватает слагаемого 4, которое дозволено взять из свободного члена:x? + 4•x + 4 – 9 ? (x + 2)? = 9

8. Извлеките квадратный корень:x + 2 = ±3 ? x1 = 1; x2 = -5.

9. Способ выделения квадрата двучлена обширно используется для облегчения массивных алгебраических выражений наравне с другими методами: группировка, замена переменной, вынесение всеобщего множителя за скобку и т.д. Полный квадрат является одной из формул сокращенного умножения и частным случаем Бинома Ньютона.