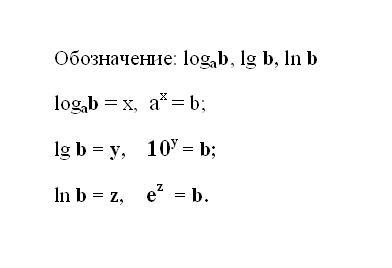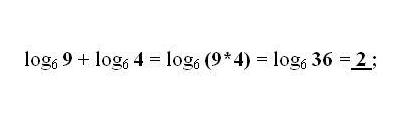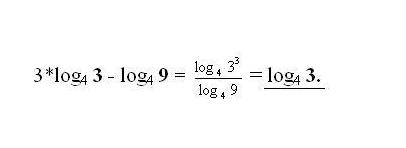Совет 1: Как решать логарифмы

Логарифм числа b определяет показатель степени для возведения начального позитивного числа a, являющегося основанием логарифма, и приобретения в итоге заданного числа b. Решение логарифма заключается в определении данной степени по заданным числам. Существует несколько базовых правил для определения логарифма либо реформирования записи логарифмического выражения. Применяя данные правила и определения дозволено вычислить логарифмические уравнения, находить производные, решать интегралы и другие выражения. Решение логарифма зачастую выглядит, как упрощенная логарифмическая запись.

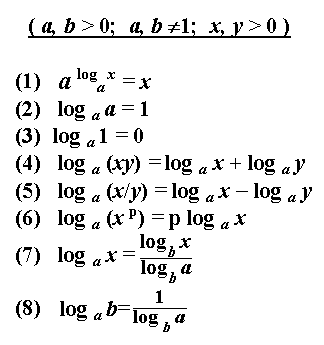
Инструкция

1. Запишите заданное логарифмическое выражение. Если в выражении применяется логарифм по основанию 10, то его запись укорачивается и выглядит так: lg b – это десятичный логарифм. Если же логарифм имеет в виде основания естественное число е, то записывают выражение: ln b – настоящий логарифм. Подразумевается, что итогом всякого логарифма является степень, в которую нужно построить число основания, дабы получилось число b.



2. Решение логарифма заключается в вычислении данной степени. Перед решением логарифмическое выражение, как водится, требуется упростить. Преобразуйте его, применяя вестимые тождества, правила и свойства логарифма.



3. Сложение и вычитание логарифмов чисел b и с по идентичным основаниям заменяется одним логарифмом с произведением либо делением чисел b и с соответственно. Применяйте по необходимости самое распространенное реформирование – формулу перехода логарифма к иному основанию.



4. Применяя выражения для облегчения логарифма, рассматривайте существующие ограничения. Так основание логарифма а может быть только правильным числом, не равным единице. Число b также должно быть огромнее нуля.

5. Впрочем не неизменно, упростив выражение, дозволено вычислить логарифм в его числовом виде. Изредка это не имеет смысла, потому что многие степени представляют собой иррациональные числа. В таком случае оставьте степень числа записанной в виде логарифма.

Совет 2: Как решать двойные интегралы

Из курса математического обзора знаменито представление двойного интеграла. Геометрически двойственный интеграл представляет собой объём цилиндрического тела на основании D и ограниченного поверхностью z = f(x, y). С поддержкой двойных интегралов дозволено рассчитать массу тонкой пластины с заданной плотностью, площадь плоской фигуры, площадь куска поверхности, координаты центра тяжести однородной пластины и другие величины.

Инструкция

1. Решение двойных интегралов дозволено свести к вычислению определённых интегралов.Если функция f(x, y) является замкнутой и постоянной в некоторой области D, ограниченной линией y = c и линией x = d, при этом c < d, а также функциями y = g(x) и y = z(x), при этом g(x), z(x) – постоянны на [c; d] и g(x) ? z(x) на этом отрезке, то вычислить двойственный интеграл дозволено по формуле, представленной на рисунке.



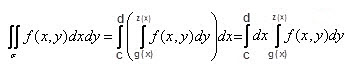
2. Если функция f(x, y) является замкнутой и постоянной в некоторой области D, ограниченной линией y = c и линией x = d, при этом c < d, а также функциями y = g(x) и y = z(x), при этом g(x), z(x) – постоянны на [c; d] и g(x) = z(x) на этом отрезке, то вычислить двойственный интеграл дозволено по формуле, представленной на рисунке.



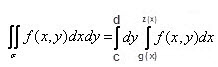
3. Если нужно вычислить двойственный интеграл на больше трудных областях D, то область D разбивается на части, всякая из которых представляет собой область, представленную в пункте 1 либо 2. Рассчитывается интеграл на всей из этих областей, полученные итоги суммируются.

Совет 3: Как решать производные

Производная – это одно из важнейших представлений не только в математике, но и во многих других областях умений. Она характеризует скорость метаморфозы функции в данный момент времени. С точки зрения геометрии, производная в некоторой точке – это тангенс угла наклона касательной к этой точке. Процесс ее нахождения именуется дифференцированием, а обратный – интегрированием. Зная несколько несложных правил, дозволено вычислять производные всяких функций, что в свою очередь значительно облегчает жизнь и химикам, и физикам, и даже микробиологам.



Вам понадобится

• учебник по алгебре за 9 класс.

Инструкция

1. Первое, что нужно для дифференцирования функций – это знать основную таблицу производных. Ее дозволено обнаружить в любом математическом справочнике.



2. Для того дабы решать задачи, связанные с нахождением производных, надобно исследовать основные правила. Выходит, возможен, у нас есть две дифференцируемы функции u и v, и некоторая непрерывна величина с. Тогда:Производная от константы неизменно равняется нулю: (с)’ = 0;Константа неизменно выносится за знак производной: (cu)’ = cu’;При нахождении производной от суммы 2-х функций, нужно легко их по очереди продифференцировать, а итоги сложить: (u+v)’ = u’+v’;При нахождении производной от произведения 2-х функций, нужно производную от первой функции умножить на вторую функцию и прибавить производную 2-й функции, умноженную на первую функцию: (u*v)’ = u’*v+v’*u;Для того, дабы обнаружить производную от частного 2-х функций нужно, из произведения производной делимого, умноженной на функцию делителя, вычесть произведение производной делителя, умноженной на функцию делимого, и все это поделить на функцию делителя возведенную в квадрат. (u/v)’ = (u’*v-v’*u)/v^2;Если дана трудная функция, то нужно перемножить производную от внутренней функции и производную от внешней. Пускай y=u(v(x)), тогда y'(x)=y'(u)*v'(x).

3. Применяя полученные выше познания, дозволено продифференцировать фактически всякую функцию. Выходит, разглядим несколько примеров:y=x^4, y’=4*x^(4-1)=4*x^3;y=2*x^3*(e^x-x^2+6), y’=2*(3*x^2*(e^x-x^2+6)+x^3*(e^x-2*x));Также встречаются задачи на вычисление производной в точке. Пускай задана функция y=e^(x^2+6x+5), необходимо обнаружить значение функции в точке х=1. 1) Обнаружьте производную функции: y’=e^(x^2-6x+5)*(2*x +6).2) Вычислите значение функции в заданной точке y'(1)=8*e^0=8

Видео по теме


Полезный совет
Выучите таблицу элементарных производных. Это невидимо сэкономит время.

Совет 4: Как решать иррациональные уравнения

Выходит, чем же отличается иррациональное уравнение от разумного? Если неведомая переменная находиться под знаком квадратного корня, то уравнение считается иррациональным.

Инструкция

1. Стержневой способ решения таких уравнений – способ возведения обоих частей уравнения в квадрат. Однако. это безусловно, первым делом нужно избавиться от знака квадратного корня. Технически данный способ не труден, но изредка это может привести к неприятностям. Скажем, уравнение v(2х-5)=v(4х-7). Построив обе его стороны в квадрат, вы получите 2х-5=4х-7. Такое уравнение решить не составит труда; х=1. Но число 1 не будет являться корнем данного уравнения . Отчего? Подставьте единицу в уравнение взамен значения х.И в правой и в левой части будут содержаться выражения, не имеющие смысла, то есть негативные. Такое значение не возможно для квадратного корня. Следственно 1 – сторонний корень, и следственно данное иррациональное уравнение не имеет корней.

2. Выходит, иррациональное уравнение решается с подмогой способа возведения в квадрат обоих его частей. И решив уравнение, нужно неукоснительно сделать проверку, дабы отсечь сторонние корни. Для этого подставьте обнаруженные корни в подлинное уравнение.

3. Разглядите еще один пример.2х+vх-3=0Конечно же, это уравнение дозволено решить по той же схеме, что и предыдущее. Перенести комбинированные уравнения , не имеющие квадратного корня, в правую часть и дальше применять способ возведения в квадрат. решить полученное разумное уравнение и проверить корни. Но существует и иной метод, больше грациозный. Введите новую переменную; vх=y. Соответственно, вы получите уравнение вида 2y2+y-3=0. То есть обыкновенное квадратное уравнение. Обнаружьте его корни; y1=1 и y2=-3/2. Дальше решите два уравнения vх=1; vх=-3/2. Второе уравнение корней не имеет, из первого находим, что х=1. Не позабудьте, о необходимости проверки корней.

Совет 5: Как решать тождества

Решать тождества довольно примитивно. Для этого требуется делать тождественные реформирования, пока поставленная цель не будет достигнута. Таким образом, при помощи простейших арифметических действий поставленная задача будет решена.



Вам понадобится

• – бумага;
• – ручка.

Инструкция

1. Примитивный пример таких реформирований – алгебраические формулы сокращенного умножения (такие как квадрат суммы (разности), разность квадратов, сумма (разность) кубов, куб суммы (разности)). Помимо того существует уйма логарифмических и тригонометрических формул, которые по своей сути являются теми же тождествами.

2. Подлинно, квадрат суммы 2-х слагаемых равен квадрату первого плюс удвоенное произведение первого на второе и плюс квадрат второго, то есть (a+b)^2= (a+b)(a+b)=a^2+ab +ba+b^2=a^2+2ab+b^2. Упростите выражение (a-b)^2 +4ab. (a-b)^2 +4ab= a^2-2ab+b^2 +4ab=a^2+2ab+b^2=(a+b)^2. В высшей математической школе, если разобраться, тождественные реформирования – первейшее из первейшего. Но там они считаются чем-то само собой разумеющимся. Цель их не неизменно облегчение выражения, а другой раз и усложнение, с целью, как теснее говорилось, достижения поставленной цели. Любая положительная разумная дробь может быть представлена в виде суммы финального числа простейших дробейPm(x)/Qn(x)=A1/(x-a)+A2/(x-a)^2+…+Ak/(x-a)^k+…+(M1x+N1)/(x^2+2px+q) +…+ (M2x+N2)/(x^2+2px+q)^s.

3. Пример. Тождественными реформированиями разложить на простейшие дроби (x^2)/(1-x^4).Разложите выражение 1-х^4=(1-x)(1+x)(x^2+1). (x^2)/(1-x^4)=A/(1-x) + B/(x+1) +(Cx+D)/(x^2+1)Приведите сумму к всеобщему знаменателю и приравняйте числители дробей в обеих частях равенства.X^2=A(x+1)(x^2+1) +B(1-x)(x^2+1)+(Cx+D)(1-x^2)Подметьте, что:При х = 1: 1 = 4А, А = 1/4;При х = – 1: 1 = 4В, В = 1/4.Показатели при x^3: A-B-C=0, откуда С=0Коэффициенты при x^2: A+B-D=1 и D=-1/2Итак, (x^2)/(1-x^4)=1/(1-x) + 1/(4(x+1)) – 1/(2(x^2+1)).

Видео по теме

Совет 6: Как решать определенные интегралы

Решение определенного интеграла неизменно сводится к приведению его первоначального выражения к табличному виду, по которому теснее дозволено легко его вычислить. Стержневой задачей же является поиск методов данного приведения.

Общие тезисы решения

Повторите по учебнику по математическому обзору либо высшей математике, что собой представляет определённый интеграл. Как вестимо, решение определенного интеграла есть функция, производная которой даст подынтегральное выражение. Данная функция именуется первообразной. По данному тезису и строится таблица основных интегралов. Определите по виду подынтегральной функции, какой из табличных интегралов подходит в данном случае. Не неизменно получается это определить сразу же. Нередко, табличный вид становится невидим только позже нескольких реформирований по облегчению подынтегральной функции.

Метод замены переменных

Если подынтегральной функцией является тригонометрическая функция, в доводе которой определенный многочлен, то испробуйте применять способ замены переменных. Для того дабы это сделать, замените многочлен, стоящий в доводе подынтегральной функции, на некоторую новую переменную. По соотношению между новой и ветхой переменной определите новые пределы интегрирования. Дифференцированием данного выражения обнаружьте новейший дифференциал в интеграле. Таким образом, вы получите новейший вид бывшего интеграла, ближний либо даже соответствующий какому-нибудь табличному.

Решение интегралов второго рода

Если интеграл является интегралом второго рода, что обозначает векторный вид подынтегральной функции, то вам будет нужно пользоваться правилами перехода от данных интегралов к скалярным. Одним из таких правил является соотношение Остроградского-Гаусса. Данный закон дозволяет перейти от потока ротора некоторой векторной функции к тройному интегралу по дивергенции данного векторного поля.

Подстановка пределов интегрирования

После нахождения первообразной нужно подставить пределы интегрирования. Вначале подставьте значение верхнего предела в выражение для первообразной. Вы получите некоторое число. Дальше вычтите из полученного числа другое число, полученное подстановкой нижнего предела в первообразную. Если один из пределов интегрирования является бесконечностью, то при подстановке ее в первообразную функцию нужно перейти к пределу и обнаружить, к чему тяготится выражение.Если интеграл является двумерным либо трехмерным, то вам придется изображать геометрически пределы интегрирования, дабы понимать, как рассчитывать интеграл. Чай в случае, скажем, трехмерного интеграла пределами интегрирования могут быть целые плоскости, ограничивающие интегрируемый объем.

Видео по теме