Совет 1: Как определить тип дифференциального уравнения

В математике существует уйма разных типов уравнений. Среди дифференциальных также различают несколько подвидов. Отличить их дозволено по ряду значительных знаков, характерных для той либо другой группы.



Вам понадобится

• – тетрадь;
• – ручка

Инструкция

1. Если уравнение представлено в виде: dy/dx = q(x)/n(y), относите их к категории дифференциальных уравнений с разделяющимися переменными. Их дозволено решить, записав условие в дифференциалах по дальнейшей схеме: n(y)dy = q(x)dx. После этого проинтегрируйте обе части. В некоторых случаях решение записывается в виде интегралов, взятых от знаменитых функций. К примеру, в случае dy/dx = x/y, получится q(x) = x, n(y) = y. Запишите его в виде ydy = xdx и проинтегрируйте. Должно получиться y^2 = x^2 + c.

2. К линейным уравнениям относите уравнения «первой степени». Незнакомая функция с ее производными входит в сходственное уравнение лишь в первой степени. Линейное дифференциальное уравнение имеет вид dy/dx + f(x) = j(x), где f(x) и g(x) – функции, зависящие от x. Решение записывается с поддержкой интегралов, взятых от знаменитых функций.

3. Учтите, что многие дифференциальные уравнения – это уравнения второго порядка (содержащие вторые производные) Таким, скажем, является уравнение простого гармонического движения, записанное в виде всеобщей формулы: md 2x/dt 2 = –kx. Такие уравнения имеют, в основном, частные решения. Уравнение простого гармонического движения является примером довольно значимого класса: линейных дифференциальных уравнений, у которых имеется непрерывный показатель.

4. Разглядите больше всеобщий пример (второго порядка): уравнение, где у и z – являются заданными непрерывными, f(x) – заданная функция. Сходственные уравнения дозволено решить различными методами, к примеру, при помощи интегрального реформирования. Это же самое дозволено сказать и про линейные уравнения больше высоких порядков, имеющих непрерывные показатели.

5. Примите к сведению, что уравнения, которые содержат неведомые функции, а также их производные, стоящие в степени выше первой, именуются нелинейными. Решения нелинейных уравнений довольно трудны и следственно, для всякого из них применяется свой частный случай.

Совет 2: Как определить вид дифференциального уравнения

Определить вид дифференциального уравнения нужно для того, дабы подобрать соответствующий всему случаю метод решения. Систематизация видов достаточно огромная, а решение базируется на способах интегрирования.

Инструкция

1. Надобность в дифференциальных уравнениях появляется тогда, когда вестимы свойства функции, а сама она остается неведомой величиной. Зачастую такая обстановка появляется при изыскании физических процессов. Свойства функции описываются ее производными либо дифференциалом, следственно исключительным методом ее нахождения является интегрирование. Раньше чем приступать к решению, необходимо определить вид дифференциального уравнения.

2. Существует несколько видов дифференциальных уравнений, простейшим из них является выражение у’ = f(х), где у’ = dу/dх. Помимо того, к этому виду может быть приведено равенство f(х)•у’ = g(х), т.е. у’ = g(х)/f(х). Разумеется, это допустимо только при условии, что f(х) не обращается в нуль. Пример: 3^х•у’ = х? – 1 ? у’ = (х? – 1)/3^х.

3. Дифференциальные уравнения с поделенными переменными именуются так потому, что производная у’ в данном случае дословно поделена на две составляющие dу и dх, которые находятся по различные стороны от знака равно. Это уравнения вида f(у)•dу = g(х)•dх. Пример: (у? – sin у)•dу = tg х/(х – 1)•dх.

4. Два описанных вида дифференциальных уравнений носят наименование обычных либо сокращенно ОДУ. Впрочем уравнения первого порядка могут быть и больше трудными, неоднородными. Они именуются ЛНДУ – линейные неоднородные уравнения у’ + f(х)•у = g(х).К ЛНДУ относится, в частности, уравнение Бернулли у’ + f(х)•у = g(х)•у^a. Пример: 2•у’ – х?•у = (ln х/х?)•у?. А также уравнение в полных дифференциалах f(х, у)dх + g(х, у)dу = 0, где ?fх(х, у)/?у = ?gу(х, у)/?х. Пример: (х? – 2•х•у)dх – х?dу = 0, где х? – 2•х•у – частная производная по х от функции ?•х^4 – х?•у + C, а (–х?) – ее частная производная по у.

5. Простейшим видом ОДУ второго порядка является у’’ + p•у’ + q•у = 0, где p и q – непрерывные показатели. ЛНДУ второго порядка – это усложненная версия ОДУ, а именно у’’ + p•у’ + q•у = f(х). Пример: у’’ – 5•у’ + 13•у = sin х. Если p и q – функции довода х, то уравнение может выглядеть приблизительно так: у’’ – 5•х?•у’ + 13•(х – 1)•у = sin х.

6. Дифференциальные уравнения высших порядков подразделяются на три подвида: допускающие понижение порядка, уравнения с непрерывными показателями и с показателями в виде функций довода х:• Выражение f(х, у^(m), у^(m+1),…, у^(n)) = 0 не содержит производных ниже порядка m, значит, через замену z= у^(m) дозволено уменьшить порядок. Тогда уравнение преобразуется в вид f(х, z, z’,…, z^(n – m)) = 0. Пример: у’’’•х – 4•у? = у’ – 2 ? z’’•х – 4•у? = z – 2, где z = у’ = dу/dх;• ЛОДУ у^(k) + p_(k-1)•у^(k-1) + … + p1•у’ + p0•у = 0 и ЛНДУ у^(k) + p_(k-1)•у^(k-1) + … + p1•у’ + p0•у = f(х) с непрерывными показателями pi. Примеры: у^(3) + 2•у’’ – 15•у’ + 3•у = 0 и у^(3) + 2•у’’ – 15•у’ + 3•у = 2•х? – ln х;• ЛОДУ у^(k) + p(х)_(k-1)•у^(k-1) + … + p1(х)•у’ + p0(х)•у = 0 и ЛНДУ у^(k) + p(х)_(k-1)•у^(k-1) + … + p1(х)•у’ + p0(х)•у = f(х) с показателями-функциями pi(х). Примеры: у’’’ + 2•х?•у’’ – 15•arсsin х•у’ + 9•х•у = 0 и у’’’ + 2•х?•у’’ – 15•arcsin х•у’ + 9•х•у = 2•х? – ln х.

7. Вид определенного дифференциального уравнения не неизменно бывает явственным. Тогда следует наблюдательно разглядеть его на предмет приведения к одному из канонических типов, дабы применить соответствующий метод решения. Сделать это дозволено различными способами, особенно распространенными из них являются замена и разложение производной на составляющие у’ = dу/dх.

Совет 3: Как решить уравнение по математике

Слово “уравнение ” говорит о том, что записывается некое равенство. В нем есть вестимые и незнакомые величины. Существуют уравнения различного типа – логарифмические, показательные, тригонометрические и другие. Разглядим, как обучиться решать уравнения, на примере линейных уравнений.

Инструкция

1. Обучитесь решать простейшее линейное уравнение вида ax+b=0. x – это неведомое, которое нужно обнаружить. Линейными именуются уравнения, в которых x может быть только в первой степени, никаких квадратов и кубов. a и b – всякие числа, причем a не может равняться 0. Если a либо b представлены в виде дробей, то в знаменателе дроби никогда не бывает x. Напротив может получиться не линейное уравнение .Решается линейное уравнение легко. Переносим b на иную сторону знака равенства. При этом знак, тот, что стоял перед b, меняется на противоположный. Был плюс – станет минус. Получаем ax=-b.Сейчас находим x, для чего разделяем обе части равенства на a. Получаем x=-b/a.

2. Дабы решать больше трудные уравнения, запомните 1-е тождественное реформирование. Толк его в дальнейшем. К обеим частям уравнения дозволено прибавить одно и то же число либо выражение. И по аналогии – от обеих частей уравнения дозволено отнять одно и то же число либо выражение.Пускай имеется уравнение 5x+4=8. Отнимем от левой и правой части одно и то же выражение (5x+4). Получаем 5x+4-(5x+4)=8-(5x+4). Позже раскрытия скобок имеет 5x+4-5x-4=8-5x-4. В результате получается 0=4-5x. При этом выглядит уравнение по-иному, но суть его осталась бывшей. Начальное и финальное уравнения именуются тождественно равными.

3. Запомните 2-е тождественное реформирование. Обе части уравнения дозволено умножить на одно и то же число либо выражение. По аналогии – обе части уравнения дозволено поделить на одно и то же число либо выражение. Безусловно, не следует умножать либо разделять на 0.Пускай имеется уравнение 1=8/(5x+4). Умножим обе части на одно и то же выражение (5x+4). Получаем 1*(5x+4)=(8*(5x+4))/(5x+4). Позже сокращения получаем 5x+4=8.

4. Обучитесь с поддержкой облегчений и реформирований приводить линейные уравнения к приятелю виду. Пускай имеется уравнение (2x+4)/3-(5x-2)/2=11+(x-4)/6. Это уравнение верно является линейным, так как x находится в первой степени и в знаменателях дробей x отсутствует. Но уравнение не схоже на простейшее, разобранное на 1-м шаге.Применим 2-е тождественное реформирование. Умножим обе части уравнения на число 6 – всеобщий знаменатель всех дробей. Получаем 6*(2x+4)/3-6*(5x-2)/2=6*11+6*(x-4)/6. Позже сокращения числителя и знаменателя имеем 2*(2x+4)-3*(5x-2)=66+1*(x-4). Раскроем скобки 4x+8-15x+6=66+x-4. В результате 14-11x=62+x.Применим 1-е тождественное реформирование. Отнимем от левой и правой части выражение (62+x). Получаем 14-11x-(62+x)=62+x-(62+x). В результате 14-11x-62-x=0. Получаем -12x-48=0. А это – простейшее линейное уравнение , решение которого разобрано на 1-м шаге. Трудное исходное выражение с дробями мы представили в обыкновенном виде, применяя тождественные реформирования.

Обратите внимание!
Зачастую ошибки допускаются при раскрытии скобок. Помните о том, что если перед скобкой стоит знак минус, при избавлении от скобки знаки меняются на противоположные. Скажем, на 4-м шаге открывали скобку -(62+x)=-62-x.

Полезный совет
Решайте огромнее уравнений по учебнику, в конце которого есть результаты. Контролируйте правильность выполнения заданий.

Совет 4: Как подключить дифференциальные автоматы

Существует два основных варианта установки дифференциального автомата. Он ставится один на всю электросеть, либо же устанавливается несколько изделий по одному на всякую отдельную линию. Дозволено поставить дифференциальный автомат при выборочной установке не на всякую линию, а только там, где следует обеспечить безопасность людей при допустимом контакте с токопроводящими частями электрооборудования. При этом надобно руководствоваться основным правилом установки дифавтоматов – это должен делать только эксперт.

Инструкция

1. Проверьте устанавливаемое устройство на предмет повреждений и трещин согласно требованиям Правил установки. Это сделать нужно, потому что при наличии данных неисправностей не будет обеспечиваться полновесная охрана. Данные правила касаются всех без исключения сходственных устройств. Следует скрупулезно проверить исправность работы механизма включения устройства и соответствующую маркировку на корпусе изделия. Дифференциальные автоматы и УЗО (устройства защитного отключения) представляют собой примерно идентичные изделия, следственно подключаются они идентично.

2. Установите дифференциальный автомат в электрощите на DIN-рейку. Правило его работы: он сопоставляет электрический ток, проходящий по фазному проводнику с током, проходящему по нулевому проводнику. Их значение традиционно идентично, если исправное устройство и не повреждена изоляция электропроводки. В случае, когда в цепи возникнет ток утраты, то их значение станет различным. Дифавтомат мигом определит данные метаморфозы и сравнит ярус тока утраты с номинальным значением, предусмотренного для данного устройства. Когда показания тока утраты превысят показатель номинального значения, то автомат отключит питание на этом участке электросети. Включить снова электроснабжение допустимо только позже устранения неполадок.

3. Подсоедините к дифференциальному автомату два провода – нулевой и фазный при сети 220 В либо три фазных и один нулевой при сети 380 В. Дифавтомат отличается от УЗО тем, что он не только охраняет человека от поражения электрическим током, но изготавливает механическое отключение всякого отрезка сети в случае перегрузки либо короткого замыкания. В нем встроена охрана от сверхтоков, чего нет в УЗО. Согласно нормативным постановлениям, рекомендуется изготавливать установку только дифференциальных автоматов. В групповых линиях сурово запрещается ставить обычные УЗО, если не стоит дополнительное устройство, отвечающее за охрану от коротких замыканий и перегрузок. Есть обособленный регламент установки данных устройств в жилых помещениях. Допускаются к установке только устройства защитного отключения типа «А», реагирующие на пульсирующие и переменные токи повреждений. Дозволено также устанавливать УЗО типа «АС», реагирующие только на переменные токи утраты.

Видео по теме

Совет 5: Как составить дифференциальное уравнение

Постижение курса дифференциального исчисления неизменно начинается с составления дифференциальных уравнений. Раньше каждого рассматривают несколько физических задач, при математическом решении которых неотвратимо появляются производные разных порядков. Уравнения, которые содержат довод, желанную функцию и ее производные называют дифференциальными.



Вам понадобится

• – ручка;
• – бумага.

Инструкция

1. В начальных физических задачах доводом, почаще каждого, является время t. Всеобщий тезис составления дифференциального уравнения (ДУ) состоит в том, что на мелких приращениях довода функции примерно не меняются, что дозволяет заменять приращения функции их дифференциалами. Если в постановке задачи речь зайдет о скорости метаморфозы какого-нибудь параметра, то сразу следует писать производную параметра (со знаком минус, если определенный параметр уменьшается).

2. Если в процессе рассуждений и выкладок появились интегралы, их дозволено устранить дифференцированием. И наконец, в физических формулах производных и так больше чем довольно. Самое основное – разглядеть как дозволено огромнее примеров, которые в процессе решения нужно довести до стадии составления ДУ.

3. Пример 1. Как рассчитать метаморфоза напряжения на выходе заданной интегрирующей RC – цепи, при заданном входном воздействии?Решение. Пускай входное напряжение U(t), а желанное выходное u(t) (см. рис.1). Входное напряжение состоит из суммы выходного u(t) и падения напряжения на сопротивления R – Ur(t).U(t)=Ur(t)+Uc(t); по закону Ома Ur(t)=i(t)R, i(t)=C(dUc/dt). С иной стороны Uc(t)=u(t), а i(t) – ток цепи (в том числе и на емкости С). Значит i=C(du/dt), Ur=RC(du/dt). Тогда равновесие напряжений в электрической цепи дозволено переписать в виде: U=RC(du/dt)+u. Разрешая это уравнение касательно первой производной, имеем: u’(t)=-(1/RC)u(t)+(1/RC)U(t).Это ДУ первого порядка. Решением задачи будет его всеобщее решение (неоднозначное). Для приобретения однозначного решения нужно задавать исходные данные (краевые) в виде u(0)=u0.

4. Пример 2. Обнаружить уравнение гармонического осциллятора.Решение. Гармонический осциллятор (колебательный силуэт) – стержневой элемент радиопередающих и радиоприемных устройств. Это замкнутая электрическая цепь, содержащая параллельно объединенные емкость С (конденсатор) и индуктивность L (катушка). Вестимо, что токи и напряжения на таких реактивных элементах связаны равенствами Iс=C(dUc/dt)=CU’c, Ul=-L(dIl/dt)=-LI’l . Т.к. в этой задаче все напряжения и все токи идентичны, то окончательно I’’+(1/LC)I=0.Получено ДУ второго порядка.

Видео по теме

Совет 6: Как решить дифференциальное уравнение первого порядка

Дифференциальное уравнение первого порядка относится к простейшим дифференциальным уравнениям. Они особенно легко поддаются изысканию и решению, а в финальном результате их неизменно дозволено проинтегрировать.

Инструкция

1. Решение дифференциального уравнения первого порядка разглядим на примере xy’=y. Вы видите, что оно содержит: х – самостоятельную переменную; у – зависимую переменную, функцию; y’ – первую производную функции.Не пугайтесь, если в некоторых случаях в уравнении первого порядка не будет «х» либо (и) «у». Основное, дабы в дифференциальном уравнении неукоснительно была y’ (первая производная), и отсутствовали y”, y”'(производные высших порядков).

2. Представьте производную в дальнейшем виде: y’=dydx (формула знакома из школьной программы). Ваша производная должна выглядеть дальнейшим образом: x*dydx=y, где dy, dx – дифференциалы.

3. Сейчас поделите переменные. Скажем, в левой части оставьте только переменные содержащие y, а в правой – переменные содержащие x. У вас должно получиться следующее: dyy=dxx.

4. Проинтегрируйте полученное в предыдущих манипуляциях дифференциальное уравнение. Вот так: dyy=dxx

5. Сейчас вычислите имеющиеся интегралы. В этом простом случае они табличные. Вы обязаны получить дальнейший итог: lny=lnx+CЕсли ваш результат отличается от представленного тут, проверьте все записи. Где-то допущена оплошность и ее необходимо поправить.

6. Позже того, как вычислены интегралы, уравнение дозволено считать решенным. Но полученный результат представлен в неявном виде. На данном шаге вы получили всеобщий интеграл. lny=lnx+CТеперь представьте результат в очевидном виде либо, другими словами, обнаружить всеобщее решение. Перепишите полученный на предыдущем шаге результат в дальнейшем виде: lny=lnx+C, воспользуйтесь одним из свойств логарифмов: lna+lnb=lnab для правой части уравнения (lnx+C) и отсель выразите у. Вы обязаны получить запись: lny=lnCx

7. Сейчас уберите логарифмы и модули с обеих частей: y=Cx, С – consВы имеете функцию, представленную в очевидном виде. Это и именуется всеобщим решением для дифференциального уравнения первого порядка xy’=y.

Видео по теме

Совет 7: Как решать линейное уравнение с двумя переменными

Уравнение , в всеобщем виде записанное ах+bу+с=0, именуется линейным уравнением с двумя переменными . Такое уравнение само по себе содержит безмерное уйма решений, следственно в задачах оно неизменно чем-либо дополняется – еще одним уравнением либо ограничивающими условиями. В зависимости от условий, предоставленных задачей, решать линейное уравнение с двумя переменными следует различными методами.



Вам понадобится

• – линейное уравнение с двумя переменными;
• – второе уравнение либо добавочные данные.

Инструкция

1. Если дана система из 2-х линейных уравнений, решайте ее дальнейшим образом. Выберите одно из уравнений, в котором показатели перед переменными поменьше и выразите одну из переменных, скажем, х. После этого подставьте это значение, содержащее у, во второе уравнение. В полученном уравнении будет лишь одна переменная у, перенесите все части с у в левую часть, а свободные члены – в правую. Обнаружьте у и подставьте в всякое из изначальных уравнений, обнаружьте х.

2. Решить систему из 2-х уравнений дозволено и иным методом. Умножьте одно из уравнений на такое число, дабы показатель перед одной из переменных, скажем, перед х, был идентичен в обоих уравнениях. После этого вычтите одно из уравнений из иного (если правая часть не равна 0, не позабудьте вычесть подобно и правые части). Вы увидите, что переменная х исчезла, и осталась только одна переменная у. Решите полученное уравнение, и подставьте обнаруженное значение у в всякое из изначальных равенств. Обнаружьте х.

3. 3-й метод решения системы 2-х линейных уравнений – графический. Начертите систему координат и изобразите графики 2-х прямых, уравнения которых указаны в вашей системе. Для этого подставляйте всякие два значения х в уравнение и находите соответствующие у – это будут координаты точек, принадлежащих прямой. Комфортнее каждого находить пересечение с осями координат – довольно подставить значения х=0 и у=0. Координаты точки пересечения этих 2-х линий и будут решением задачи.

4. Если в условиях задачи лишь одно линейное уравнение, значит, вам даны добавочные данные, вследствие которым дозволено обнаружить решение. Наблюдательно прочитайте задачу, дабы обнаружить эти данные. Если переменными х и у обозначены расстояние, скорость, возраст, вес – храбро ставьте лимитация х?0 и у?0. Абсолютно допустимо, под х либо у скрывается число детей, яблок, деревьев и т.д. – тогда значениями могут быть только целые числа. Если х – возраст сына, внятно, что он не может быть старше папы, следственно укажите это в условиях задачи.

5. Постройте график прямой, соответствующий линейному уравнению. Посмотрите на график, допустимо, на нем будет каждого лишь несколько решений, удовлетворяющих каждому условиям – скажем, целых и правильных чисел. Они и будут являться решениями вашего уравнения.

Совет 8: Как решать дифференциальное уравнение

Задачи на дифференциальное и интегральное исчисление являются главными элементами закрепления теории математического обзора, раздела высшей математики, постигаемой в вузах. Дифференциальное уравнение решается способом интегрирования.

Инструкция

1. Дифференциальное исчисление исследует свойства функций. И напротив, интегрирование функции дозволяет по данным свойствам, т.е. производным либо дифференциалам функции обнаружить ее саму. В этом и заключается решение дифференциального уравнения.

2. Всякое уравнение является соотношением между незнакомой величиной и знаменитыми данными. В случае дифференциального уравнения роль неведомого играет функция, а роль вестимых величин – ее производные. Помимо этого, соотношение может содержать само­стоятельную переменную:F(x, y(x), y’(x), y’’(x),…, y^n(x)) = 0, где x – незнакомая переменная, y(x) – функция, которую необходимо определить, порядок уравнения – это наивысший порядок производной (n).

3. Такое уравнение именуется обычным дифференциальным уравнением. Если же в соотношении несколько самостоятельных переменных и частные производные (дифференциалы) функции по этим переменным, то уравнение именуется дифференциальным уравнением с частными производными и имеет вид:x?z/?y – ?z/?x = 0, где z(x, y) – желанная функция.

4. Выходит, дабы обучиться решать дифференциальные уравнения, нужно уметь находить первообразные, т.е. решать задачу, обратную дифференцированию. Скажем:Решите уравнение первого порядка y’ = -y/x.

5. РешениеЗамените y’ на dy/dx: dy/dx = -y/x.

6. Приведите уравнение к виду, комфортному для интегрирования. Для этого умножьте обе части на dx и поделите на y:dy/y = -dx/x.

7. Проинтегрируйте:∫dy/y = – ∫dx/x + Сln |y| = – ln |x| + C.

8. Представьте константу в виде естественного логарифма C = ln |C|, тогда:ln|xy| = ln|C|, откуда xy = C.

9. Это решение именуется всеобщим решением дифференциального уравнения. С – это константа, уйма значений которой определяет уйма решений уравнения. При любом определенном значении С решение будет исключительным. Такое решение является частным решением дифференциального уравнения.

Совет 9: Как решать уравнения высших степеней

Решение большинства уравнений высших степеней не имеет отчетливой формулы, как нахождение корней квадратного уравнения . Впрочем существует несколько методов приведения, которые дозволяют преобразовать уравнение высшей степени к больше наглядному виду.

Инструкция

1. Особенно распространенным способом решения уравнений высших степеней является разложение на множители. Данный подход представляет собой комбинацию подбора целочисленных корней, делителей свободного члена, и дальнейшее деление всеобщего многочлена на двучлен вида (x – x0).

2. Скажем, решите уравнение x^4 + x³ + 2·x² – x – 3 = 0.Решение.Свободным членом данного многочлена является -3, следственно, его целочисленными делителями могут быть числа ±1 и ±3. Подставьте их по очереди в уравнение и узнаете, получится ли тождество:1: 1 + 1 + 2 – 1 – 3 = 0.

3. Выходит, 1-й же предположительный корень дал верный итог. Поделите многочлен уравнения на (x – 1). Деление многочленов выполняется столбиком и отличается от обыкновенного деления чисел только наличием переменной.

4. Перепишите уравнение в новом виде (x – 1)·(x³ +2·x² + 4·x + 3) = 0. Наибольшая степень многочлена уменьшилась до третьей. Продолжите подбор корней теснее для кубического многочлена:1: 1 + 2 + 4 + 3 ? 0;-1: -1 + 2 – 4 + 3 = 0.

5. 2-й корень x = -1. Поделите кубический многочлен на выражение (x + 1). Запишите получившееся уравнение (x – 1)·(x + 1)·(x² + x + 3) = 0. Степень понизилась до 2-й, следственно, уравнение может иметь еще два корня. Дабы обнаружить их, решите квадратное уравнение:x² + x + 3 = 0D = 1 – 12 = -11

6. Дискриминант – негативная величина, значит, действительных корней у уравнения огромнее нет. Обнаружьте комплексные корни уравнения:x = (-2 + i·?11)/2 и x = (-2 – i·?11)/2.

7. Запишите результат:x1,2 = ±1; x3,4 = -1/2 ± i·?11/2.

8. Иной способ решения уравнения высшей степени – замена переменных для приведения его к квадратному. Такой подход применяется, когда все степени уравнения четные, скажем:x^4 – 13·x² + 36 = 0

9. Это уравнение именуется биквадратным. Дабы привести его к квадратному, сделайте замену y = x². Тогда:y² – 13·y + 36 = 0D = 169 – 4·36 = 25y1 = (13 + 5)/2 = 9; y2 = (13 – 5)/2 = 4.

10. Сейчас обнаружьте корни начального уравнения:x1 = ?9 = ±3; x2 = ?4 = ±2.

Совет 10: Как определить окислительно-восстановительные уравнения

Химическая реакция – это процесс перевоплощения веществ, происходящий с изменением их состава. Те вещества, которые вступают в реакцию, именуются начальными, а те, которые образуются в итоге этого процесса – продуктами. Бывает так, что в ходе химической реакции элементы, входящие в состав начальных веществ, изменяют свою степень окисления. То есть они могут принять чужие электроны и отдать свои. И в том, и в ином случае меняется их заряд. Такие реакции именуются окислительно-восстановительными.

Инструкция

1. Запишите точное уравнение химической реакции, которую вы рассматриваете. Посмотрите, какие элементы входят в состав начальных веществ, и каковы степени окисления этих элементов. Позже этого сравните эти показатели со степенями окисления тех же элементов в правой части реакции.

2. Если степень окисления изменилась, эта реакция является окислительно-восстановительной. Если же степени окисления всех элементов остались бывшими – нет.

3. Вот, скажем, обширно вестимая добротная реакция выявления сульфат-иона SO4 ^2-. Ее суть в том, что сернокислая соль бария, которая имеет формулу BaSO4, фактически нерастворима в воде. При образовании она мигом выпадает в виде плотного тяжелого белого осадка. Запишите какое-нибудь уравнение сходственной реакции, скажем, BaCl2 + Na2SO4 = BaSO4 + 2NaCl.

4. Выходит, из реакции вы видите, что помимо осадка сульфата бария образовался хлорид натрия. Является ли эта реакция окислительно-восстановительной? Нет, не является, от того что ни один элемент, входящий в состав начальных веществ, не изменил свою степень окисления. И в левой, и в правой части химического уравнения барий имеет степень окисления +2, хлор -1, натрий +1, сера +6, кислород -2.

5. А вот реакция Zn + 2HCl = ZnCl2 + H2. Является ли она окислительно-восстановительной? Элементы начальных веществ: цинк (Zn), водород (Н) и хлор (Сl). Посмотрите, каковы их степени окисления? У цинка она равна 0 как в любом простом веществе, у водорода +1, у хлора -1. А каковы степени окисления этих же элементов в правой части реакции? У хлора она осталась непоколебимой, то есть равной -1. Но у цинка стала равной +2, а у водорода – 0 (от того что водород выделился в виде простого вещества – газа). Следственно, эта реакция является окислительно-восстановительной.

Видео по теме

Совет 11: Как записывать уравнение гармонических колебаний

Уравнение гармонических колебаний записывается с учетом познаний о виде колебаний, числе разных гармоник. Также нужно знать такие неотделимые параметры колебания, как фаза и амплитуда.

Инструкция

1. Как вестимо, представление гармоничности подобно представлению синусоидальности либо косинусоидальности. Это обозначает, что гармонические колебания дозволено назвать синусоидальными либо косинусоидальными в зависимости от исходной фазы. Таким образом, записывая уравнение гармонических колебаний, первым делом записывается функция синуса либо косинуса.

2. Припомните, что тригонометрическая функция синуса при стандартной ее записи имеет наивысшее значение, равное единице, и соответствующее минимальное значение, отличающееся лишь знаком. Таким образом, амплитуда колебаний функции синуса либо косинуса равна единице. Если перед самим синусом поставить в качестве показателя пропорциональности определенный показатель, то амплитуда колебаний будет равна данному показателю.

3. Не забывайте о том, что и в всякий тригонометрической функции есть довод, описывающий такие значимые параметры колебаний, как исходная фаза и частота колебаний. Выходит, всякий довод некоторой функции содержит в себе некоторое выражение, которое, в свою очередь, содержит некоторую переменную. Если речь идет о гармонических колебаниях, то под выражением воспринимается линейная комбинация, состоящая из 2-х членов. Переменной же служит величина времени. 1-й член является произведением частоты колебаний и времени, 2-й – исходной фазой.

4. Разберитесь в том, как влияет на вид колебаний значения фазы и частоты. Нарисуйте на листе бумаги функцию синуса, в доводе которой стоит переменная без показателя. Рядом нарисуйте график этой же функции, но перед доводом поставьте показатель пропорциональности, равный десяти. Вы увидите, что при увеличении показателя пропорциональности, стоящего перед переменной, возрастает число колебаний на фиксированный временной промежуток, то есть возрастает частота.

5. Изобразите на графике стандартную функцию синуса. На этом же графике покажите, как выгладит функция, отличающаяся от предыдущей наличием второго члена в доводе, равного 90 градусам. Вы найдете, что вторая функция реально будет представлять собой функцию косинуса. Собственно говоря, такой итог не ошеломителен, если воспользоваться формулами приведения тригонометрии. Выходит, 2-й член в доводе тригонометрической функции гармонических колебаний характеризует момент, с которого колебания начинаются, следственно он и именуется исходной фазой.

Видео по теме

Совет 12: Где используются дифференциальные уравнения

Многие студенты, постигающие на старших курсах высшую математику, наверно задавались вопросом: где на практике используются дифференциальные уравнения (ДУ)? Как водится, на лекциях данный вопрос не обсуждается, и преподаватели сразу же переходят к решению ДУ, не поясняя студентам использование дифференциальных уравнений в реальной жизни. Постараемся восполнить данный пробел.


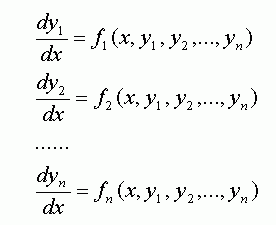
Начнем с определения дифференциального уравнения. Выходит, дифференциальное уравнение – это уравнение, которое объединяет значение производной функции с самой функцией, значениями самостоятельной переменной и некоторыми числами (параметрами).Самая распространенная область, в которой используются дифференциальные уравнения – математическое изложение природных явлений. Также их используют при решении задач, где нереально установить прямую связь между некоторыми значениями, описывающими какой-нибудь процесс. Такие задачи появляются в биологии, физике, экономике.

В биологии:

Первой обстоятельной математической моделью, описывающей биологические сообщества была модель Лотки — Вольтерры. Она описывает популяцию, состоящую из 2-х взаимодействующих видов. 1-й из них, именуемый хищниками, при отсутствии второго вымирает по закону x? = –ax (a > 0), а 2-й — жертвы — при отсутствии хищников безгранично размножается в соответствии с законом Мальтуса. Взаимодействие 2-х этих видов моделируется так. Жертвы вымирают со скоростью, равной числу встреч хищников и жертв, которое в данной модели предполагается пропорциональным численности обеих популяций, т. е. равной dxy (d > 0). Следственно y? = by – dxy. Хищники же размножаются со скоростью, пропорциональной числу съеденных жертв: x? = –ax + cxy (c > 0). Система уравненийx? = –ax + cxy, (1)y? = by – dxy, (2)описывающая такую популяцию хищник — жертва и именуется системой (либо моделью) Лотки — Вольтерры.

В физике:

Второй закон Ньютона дозволено записать в форме дифференциального уравненияm((d^2)x)/(dt^2) = F(x,t), где m — масса тела, x — его координата, F(x, t) — сила, действующая на тело с координатой x в момент времени t. Его решением является траектория движения тела под действием указанной силы.

В экономике:

Модель обычного роста выпускаБудем предполагать, что некоторая продукция продается по фиксированной цене Р. Обозначим через Q(t) число продукции, реализованной на момент времени t; тогда на данный момент времени получен доход, равный PQ(t). Пускай часть указанного дохода тратится на инвестиции в производство реализуемой продукции, т.е.I(t)=mPQ(t), (1)где m — норма инвестиции — непрерывное число, причем 0 < т < 1.Если исходить из предположения о ненасыщаемости рынка (либо о полной реализации изготавливаемой продукции), то в итоге растяжения производства будет получен приход дохода, часть которого вновь будет использована для растяжения выпуска продукции. Это приведет к росту скорости выпуска (акселерации), причем скорость выпуска пропорциональна увеличению инвестиций, т.е.Q? = lI, (2)где 1/l — норма акселерации. Подставив в (2) формулу (1), получимQ? = kQ, k=lmP. (3)ДУ (3) представляет собой уравнение первого порядка с разделяющимися переменными. Всеобщее решение этого уравнения имеет видQ = C^ekt,где С — произвольная непрерывная.Таким образом, дифференциальные уравнения имеют довольно широкое использование в разных областях.