Совет 1: Как определить периодичность функции

По школьным урокам математики всякий помнит график синуса, равномерными волнами уходящий вдаль. Аналогичным свойством — повторяться через определенный интервал — владеют и многие другие функции. Они именуются периодическими. Периодичность — дюже значимое качество функции, зачастую встречающееся в разных задачах. Следственно благотворно уметь определять, является ли функция периодической.

Инструкция

1. Если F(x) — функция довода x, то она именуется периодической, если есть такое число T, что для всякого x F(x + T) = F(x). Это число T и именуется периодом функции.Периодов может быть и несколько. Скажем, функция F = const для всяких значений довода принимает одно и то же значение, а потому всякое число может считаться ее периодом.Традиционно математика волнует минимальный не равный нулю период функции. Его для краткости и называют примитивно периодом.

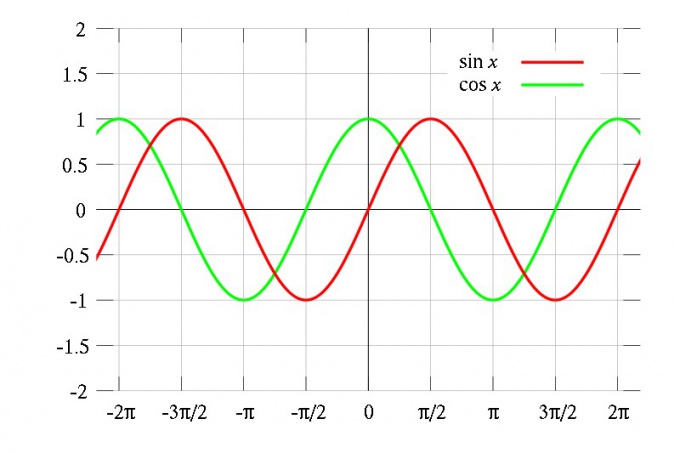
2. Типичный пример периодических функций — тригонометрические: синус, косинус и тангенс. Их период идентичен и равен 2?, то есть sin(x) = sin(x + 2?) = sin(x + 4?) и так дальше. Впрочем, разумеется, тригонометрические функции — не исключительные периодические.

3. Касательно примитивных, базовых функций исключительный метод установить их периодичность либо непериодичность — вычисления. Но для трудных функций теснее есть несколько примитивных правил.

4. Если F(x) — периодическая функция с периодом T, и для нее определена производная, то эта производная f(x) = F?(x) — тоже периодическая функция с периодом T. Чай значение производной в точке x равно тангенсу угла наклона касательной графика ее первообразной в этой точке к оси абсцисс, а от того что первообразная периодично повторяется, то должна повторяться и производная. Скажем, производная от функции sin(x) равна cos(x), и она периодична. Беря производную от cos(x), вы получите –sin(x). Периодичность сохраняется постоянно.Впрочем обратное не неизменно правильно. Так, функция f(x) = const периодическая, а ее первообразная F(x) = const*x + C — нет.

5. Если F(x) — периодическая функция с периодом T, то G(x) = a*F(kx + b), где a, b, и k — константы и k не равно нулю — тоже периодическая функция, и ее период равен T/k. Скажем sin(2x) — периодическая функция, и ее период равен ?. Наглядно это дозволено представить так: умножая x на какое-либо число, вы как бы сжимаете график функции по горизонтали именно в столько раз

6. Если F1(x) и F2(x) — периодические функции, и их периоды равны T1 и T2 соответственно, то сумма этих функций тоже может быть периодической. Впрочем ее период не будет легкой суммой периодов T1 и T2. Если итог деления T1/T2 — разумное число, то сумма функций периодична, и ее период равен наименьшему всеобщему кратному (НОК) периодов T1 и T2. Скажем, если период первой функции равен 12, а период 2-й — 15, то период их суммы будет равен НОК (12, 15) = 60.Наглядно это дозволено представить так: функции идут с различной «шириной шага», но если отношение их ширин осмысленно, то рано либо поздно (а вернее, именно через НОК шагов), они вновь сравняются, и их сумма начнет новейший период.

7. Впрочем если соотношение периодов иррационально, то суммарная функция не будет периодической совсем. Скажем, пускай F1(x) = x mod 2 (остаток от деления x на 2), а F2(x) = sin(x). T1 тут будет равен 2, а T2 равен 2?. Соотношение периодов равняется ? — иррациональному числу. Следственно, функция sin(x) + x mod 2 не является периодической.

Совет 2: Как определить период по графику

Многие математические функции имеют одну специфика, облегчающую их построение, – это периодичность , то есть повторяемость графика на координатной сетке через равные интервалы.

Инструкция

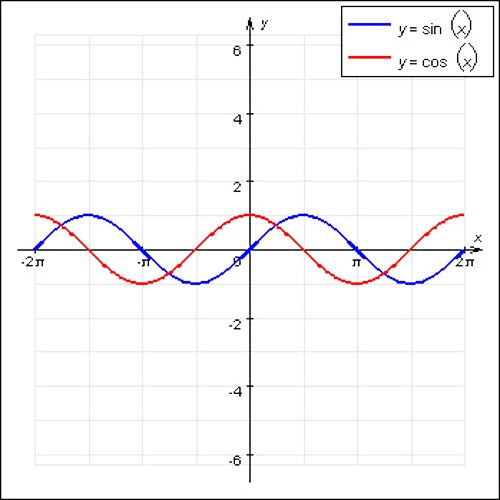
1. Самыми вестимыми периодическими функциями математики являются синусоида и косинусоида. Эти функции имеют волнообразный нрав и стержневой период, равный 2П. Также частным случаем периодической функции является f(x)=const. На позицию х подходит всякое число, основного периода данная функция не имеет, потому что представляет собой прямую.

2. Вообще функция является периодической, если существует такое целое число N, которое отменно от нуля и удовлетворяет правилу f(x)=f(x+N), таким образом обеспечивая повторяемость. Период функции – это и есть наименьшее число N, но не нуль. То есть, скажем, функция sin x равна функции sin (x+2ПN), где N=±1, ±2 и т.д.

3. Изредка при функции может стоять множитель (скажем sin 2x), тот, что увеличит либо сократит период функции. Для того дабы обнаружить период по графику , нужно определить экстремумы функции – самую высокую и самую низкую точки графика функции. Потому что синусоида и косинусоида имеют волнообразный нрав, это довольно легко сделать. От данных точек постройте перпендикулярные прямые до пересечения с осью Х.

4. Расстояние от верхнего экстремума до нижнего будет половиной периода функции. Комфортнее каждого вычислять период от пересечения графика с осью Y и, соответственно, нулевой отметки по оси х. Позже этого нужно умножить полученное значение на два и получить стержневой период функции.

5. Для простоты построения графиков синусоиды и косинусоиды нужно подметить, что если при функции стоит целое число, то ее период удлинится (то есть 2П необходимо умножить на этот показатель) и график будет выглядеть больше мягко, плавно; а если число дробное, напротив, сократится и график станет больше «острым», скачкообразным на вид.

Видео по теме