Совет 1: Как обнаружить высоту в верной пирамиде
Пирамида представляет собой многогранник, в основании которого лежит многоугольник, а грани его представляют собой треугольники, владеющие всеобщей вершиной. Для положительной пирамиды объективно то же определение, но в основании ее лежит положительный многоугольник. Под высотой пирамиды подразумевается отрезок, тот, что проведен от вершины пирамиды к основанию, и данный отрезок перпендикулярен ему. Обнаружить высоту в верной пирамиде дюже легко.
Вам понадобится
- В зависимости от обстановки, знать объем пирамиды, площадь боковых граней пирамиды, длину ребра, длину диаметра многоугольника в основании.
Инструкция
1. Одним из методов обнаружить высоту пирамиды, и не только верной – это выразить ее через объем пирамиды. Формула, по средствам которой дозволено узнать ее объем, выглядит так:V = (S*h)/3, где S – площадь всех боковых граней пирамиды в сумме, h – высота данной пирамиды.Тогда из этой формулы дозволено вывести иную, для нахождения высоты пирамиды:h = (3*V)/SК примеру, вестимо, что площадь боковых граней пирамиды 84 см?, а объем пирамиды равен 336 куб.см. Тогда обнаружить высоту дозволено так:h = (3*336)/84 = 12 смОтвет: высота данной пирамиды 12 см
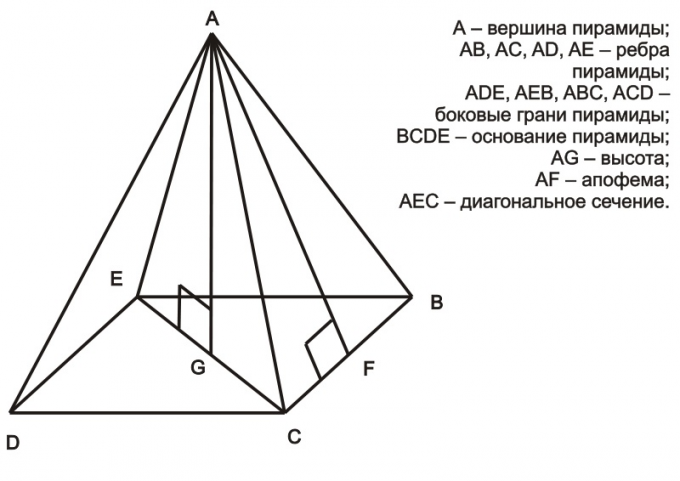
2. Рассматривая верную пирамиду, в основании которой лежит верный многоугольник, дозволено прийти к итогу, что треугольник, образованный высотой, половиной диагонали и одной из граней пирамиды, представляет из себя прямоугольный треугольник (скажем, это треугольник АEG на рисунке выше). Согласно теореме Пифагора, квадрат гипотенузы равен сумме квадратов катетов (a? = b? + c?). В случае с верной пирамидой, гипотенуза – это грань пирамиды, один из катетов – половина диагонали многоугольника в основании, а иной катет – высота пирамиды. В таком случае, зная длину грани и диагонали, дозволено вычислить и высоту . В качестве примера дозволено разглядеть треугольник AEG:AE? = EG?+GA?Отсель высоту пирамиды GA дозволено выразить так:GA = ?(AE?-EG?).
3. Дабы было больше внятно, как находить высоту положительной пирамиды, дозволено разглядеть пример: в верной пирамиде длина грани 12 см, длина диагонали многоугольника в основании – 8 см. Исходя из этих данных, требуется обнаружить длину высоты этой пирамиды.Решение: 12? = 4? + c?, где с – незнакомый катет (высота) данной пирамиды (прямоугольного треугольника).144 = 16 + 128Таким образом, высота данной пирамиды ?128 либо, примерно, 11.3 см
Совет 2: Как обнаружить площадь грани в пирамиде
Пирамида – одна из самых необъяснимых фигур в геометрии. С ней объединяют потоки космической энергии, многие древние народы избирали именно эту форму для строительства своих культовых сооружений. Тем не менее, с точки зрения математики, пирамида – это каждого лишь многогранник, с многоугольником в основании, а гранями являются треугольники с всеобщей вершиной. Разглядим, как обнаружить площадь грани в пирамиде.

Вам понадобится
- калькулятор.
Инструкция
1. Пирамиды бывают следующих типов: положительная (в основании – положительный многоугольник, а проекция вершины пирамиды на основание – его центр), произвольная (в основании лежит всякий многоугольник, а проекция вершины необязательно совпадает с его центром), прямоугольная (одно из боковых ребер составляет с основанием прямой угол) и усеченная. В зависимости от того, сколько сторон имеет многоугольник в основании пирамиды, ее называют 3-, четырех-, пяти либо, к примеру, десятиугольной.
2. От того что боковая грань всякий пирамиды (помимо усеченной) – это треугольник, нахождение площади грани сводится к определению его площади. В усеченной пирамиде боковая грань – трапеция. Выходит, разберемся, как обнаружить площадь грани пирамиды в всяком отдельном случае.
3. Для всех видов пирамид, помимо усеченной:Перемножьте длины основания треугольника и опущенной на него высоты из вершины пирамиды. Поделите полученное произведение на 2 – это и будет желанная площадь боковой грани пирамиды.
4. Усеченная пирамидаСложите оба основания трапеции, являющейся гранью такой пирамиды. Поделите полученную сумму на два. Умножьте полученное значение на высоту грани -трапеции. Полученная в итоге величина – площадь боковой грани пирамиды данного типа.
Видео по теме
Полезный совет
Площадь боковой поверхности и основания, периметр основания пирамиды и ее объем объединяют между собой определенные формулы. Это порой дает вероятность вычислить значения недостающих данных, нужных для определения площади грани в пирамиде.Объем всякий не усеченной пирамиды равен трети от произведения высоты пирамиды и площади основания. Для положительной пирамиды объективно: площадь боковой поверхности равна половине периметра основания умноженного на высоту одной из граней. При расчете объема усеченной пирамиды, взамен площади основания подставляется величина, равная сумме площадей верхнего, нижнего основания и квадратного корня из их произведения.
Совет 3: Как обнаружить объем прямоугольной пирамиды
Прямоугольной именуется пирамида, одно из ребер которой перпендикулярно ее основанию, то есть стоит под углом 90?. Это ребро является единовременно и высотой прямоугольной пирамиды. Формулу объема пирамиды впервой вывел Архимед.

Вам понадобится
- – ручка;
- – бумага;
- – калькулятор.
Инструкция
1. В прямоугольной пирамиде высотой будет ее ребро, которое стоит под углом 90? к основанию. Как водится, площадь основания прямоугольной пирамиды обозначают как S, а высоту, которая единовременно является ребром пирамиды , ? h. Тогда, дабы обнаружить объем этой пирамиды , нужно площадь ее основания умножить на высоту и поделить на 3. Таким образом, объем прямоугольной пирамиды вычисляется с подмогой формулы: V=(S*h)/3.
2. Прочитайте условие задачи. Возможен, дана прямоугольная пирамида ABCDES. В ее основании лежит пятиугольник, площадь которого 45 см?. Длина высоты SE равна 30 см.
3. Постройте пирамиду, следуя заданным параметрам. Ее основание обозначьте латинскими буквами ABCDE, а вершину пирамиды – S. Потому что чертеж получится на плоскости в проекции, то для того, дабы не запутаться, обозначьте теснее знаменитые вам данные: SE=30см; S(ABCDE)=45 см?.
4. Вычислите объем прямоугольной пирамиды , применяя формулу. Подставив данные и сделав подсчеты, получится, что объем прямоугольной пирамиды будет равен: V=(45*30)/3=см?.
5. Если в условии задачи нет данных о площади основания и высоте пирамиды , то надобно провести добавочные вычисления для приобретения этих величин. Площадь основания будет вычисляться в зависимости от того, какой многоугольник лежит в ее основании.
6. Высоту пирамиды узнаете, если знаменита гипотенуза всякого из прямоугольных треугольников EDS либо EAS и угол, под которым наклонена боковая грань SD либо SA к ее основанию. Вычислите катет SE по теореме синусов. Он и будет являться высотой прямоугольной пирамиды .
Обратите внимание!
Проводя вычисления таких величин, как высота, объем, площадь, следует помнить, что всякая из них имеет свою единицу измерения. Так, площадь измеряется в см?, высота – в см, а объем – в см?. Кубический сантиметр – это единица объема, которая равна объему куба с длиной ребер в 1см. Если подставить данные в нашу формулу, получим: см?= (см?*см)/3.
Полезный совет
Как водится, если в задаче требуется обнаружить объем прямоугольной пирамиды, то все нужные данные знамениты – как минимум для того, дабы обнаружить площадь основания и высоту фигуры.









