Совет 1: Как обнаружить уравнение касательной к графику функции

Эта инструкция содержит результат на вопрос, как обнаружить уравнение касательной к графику функции. Приведена доскональная справочная информация. Использование теоретических выкладок разобрано на определенном примере.

Инструкция

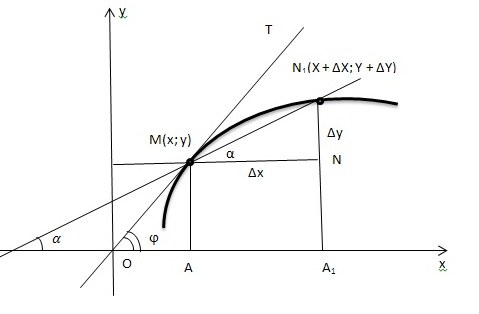
1. Справочный материал.Для начала дадим определение касательной. Касательной к косой в данной точке М именуется предельное расположение секущей NM, когда точка N приближается по косой к точке М.Обнаружим уравнение касательной к графику функции y = f(x).

2. Определяем угловой показатель касательной к косой в точке М. Кривая, представляющая собой график функции y = f(x), постоянна в некоторой окрестности точки М (включая саму точку М).Проведем секущую MN1, образующую с позитивным направлением оси Ox угол ?.Координаты точки М (x; y), координаты точки N1(x+?x; y+?y). Из полученного треугольника MN1N дозволено обнаружить угловой показатель этой секущей: tg ? = ?y/?xMN = ?xNN1 = ?yПри тяготении точки N1 по косой к точке M секущая MN1 поворачивается вокруг точки M, причем угол ? тяготится к углу ? между касательной MT и позитивным направлением оси Ox. k = tg ? =? lim??(?x?0)?? ? ?y/?x = f`(x)Таким образом, угловой показатель касательной к графику функции равен значению производной этой функции в точке касания. В этом заключается геометрический толк производной.

3. Уравнение касательной к заданной косой в заданной точке М имеет вид: y – y0 = f`(x0) (x – x0),где (x0; y0) – координаты точки касания, (x; y) – нынешние координаты, т.е. координаты всякий точки, принадлежащей касательной, f`(x0) = k = tg ? – угловой показатель касательной.

4. Обнаружим уравнение касательной на примере.Дан график функции y=x2 – 2x. Надобно обнаружить уравнение касательной в точке с абсциссой x0 = 3.Из уравнения данной косой находим ординату точки касания y0 = 32 – 2?3 = 3.Находим производную, а после этого вычисляем ее значение в точке x0 = 3.Имеем: y`=2x – 2f`(3) = 2?3 – 2 = 4.Сейчас, зная точку (3; 3) на косой и угловой показатель f`(3) = 4 касательной в этой точке, получаем желанное уравнение:y – 3 = 4 (x – 3) либо y – 4x + 9 = 0

Совет 2: Как обнаружить касательное уравнение

В учебнике 11 класса по алгебре учащиеся проходят тему производных. И вот в этом большом параграфе специальное место уделено для выяснения, что же такое касательная к графику, и как обнаружить и составить ее уравнение.

Инструкция

1. Пускай даны функция y=f(x) и определенная точка М с координатами а и f(a). И пускай вестимо, что существует f'(a). Ссоставим уравнение касательной. Это уравнение, как уравнение всякий иной прямой, которая не параллельна оси ординат, имеет вид y=kx+m, следственно для его составления нужно обнаружить неведомые k и m. С угловым показателем все ясно. Если М принадлежит графику и если от нее дозволено провести касательную, не перпендикулярную к оси абсцисс, то угловой показатель k равен f'(a). Для вычисления неведомого m используем то, что желанная прямая проходит через точку М. Следственно, если подставить координаты точки в уравнение прямой, то получим правильное равенство f(a)=ka+m. отсель находим, что m=f(a)-ka. Осталось только подставить значения показателей в уравнение прямой.y=kx+my=kx+(f(a)-ka)y=f(a)+f'(a)(x-a)Из этого следует, что уравнение имеет вид y=f(a)+f'(a)(x-a).

2. Для того, дабы обнаружить уравнение касательной к графику применяют определенный алгорифм. Во-первых, обозначьте х буквой а. Во-вторых, вычислите f(a). В третьих, обнаружьте производную от х и вычислите f'(a). И наконец, подставьте обнаруженные а, f(a) и f'(a) в формулу y=f(a)+f'(a)(x-a).

3. Для того, дабы отменнее осознать, как применять алгорифм, разглядите следующую задачу. Составьте уравнение касательной для функции y=1/x в точке х=1.Для решения этой задачи воспользуйтесь алгорифмом составления уравнения. Но при этом рассматривайте, что в данном примере дана функция f(x)=2-х-х3, а=0.1. В условии задачи указано значение точки а;2. Следственно, f(a)=2-0-0=2;3. f'(x)=0-1-3х=-1-3х; f'(a)=-1;4. Подставьте обнаруженные числа в уравнение касательной к графику: y=f(a)+f'(a)(x-a)=2+(-1)(х-0)=2-х.Результат: y=2-х.

Полезный совет
Для подтверждения вы можете возвести график функции и обнаруженной прямой.

Совет 3: Как написать уравнение касательной

Касательная к косой — прямая, которая прилегает к этой косой в заданной точке, то есть проходит через нее так, что на маленьком участке вокруг этой точки дозволено без специальной потери точности заменить кривую на отрезок касательной. Если эта кривая является графиком функции, то касательную к ней дозволено возвести по особому уравнению.

Инструкция

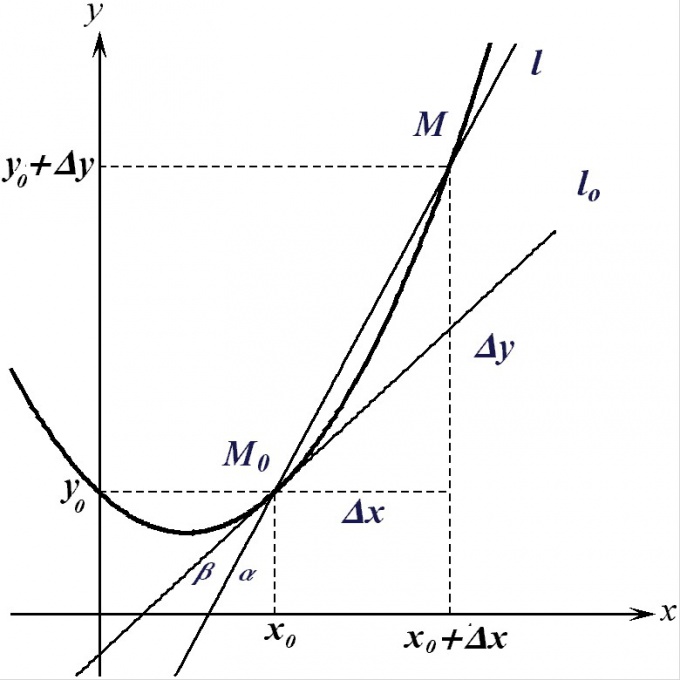
1. Представим, что у вас есть график некоторой функции. Через две точки, лежащие на этом графике, дозволено провести прямую. Такая прямая, пересекающая график заданной функции в 2-х точках, именуется секущей.Если, оставляя первую точку на месте, потихоньку двигать в ее направлении вторую точку, то секущая понемножку станет поворачиваться, тяготясь к какому-то определенному расположению. В конце концов, когда две точки сольются в одну, секущая будет плотно прилегать к вашему графику в этой исключительной точке. Иными словами, секущая превратится в касательную.

2. Любая наклонная (то есть не вертикальная) прямая на координатной плоскости является графиком уравнения y = kx + b. Секущая, проходящая через точки (x1, y1) и (x2, y2), должна, таким образом, соответствовать условиям:kx1 + b = y1, kx2 + b = y2.Решая эту систему 2-х линейных уравнений, получаем: kx2 – kx1 = y2 – y1. Таким образом, k = (y2 – y1)/(x2 – x1).

3. Когда расстояние между x1 и x2 тяготится к нулю, разности превращаются в дифференциалы. Таким образом, в уравнении касательной, проходящей через точку (x0, y0) показатель k будет равен ?y0/?x0 = f?(x0), то есть значению производной от функции f(x) в точке x0.

4. Дабы узнать показатель b, подставим теснее вычисленное значение k в уравнение f?(x0)*x0 + b = f(x0). Решая это уравнение касательно b, мы получим, что b = f(x0) – f?(x0)*x0.

5. Окончательный вариант уравнения касательной к графику заданной функции в точке x0, выглядит так:y = f?(x0)*(x – x0) + f(x0).

6. В качестве примера разглядим уравнение касательной к функции f(x) = x^2 в точке x0 = 3. Производная от x^2 равна 2x. Следственно, уравнение касательной приобретает вид:y = 6*(x – 3) + 9 = 6x – 9.Правильность этого уравнения легко проверить. График прямой y = 6x – 9 проходит через ту же точку (3;9), что и начальная парабола. Возведя оба графика, вы сумеете удостовериться, что эта прямая подлинно прилегает к параболе в этой точке.

7. Таким образом, график функции имеет касательную в точке x0 только тогда, когда функция имеет производную в этой точке. Если в точке x0 функция владеет обрывом второго рода, то касательная превращается в вертикальную асимптоту. Впрочем одно только присутствие производной в точке x0 еще не гарантирует обязательного существования касательной в этой точке. Скажем, функция f(x) = |x| в точке x0 = 0 постоянна и дифференцируема, но провести касательную к ней в этой точке немыслимо. Стандартная формула в этом случае дает уравнение y = 0, но эта прямая не является касательной к графику модуля.

Совет 4: Как обнаружить абсциссу точки касания

При составлении уравнения касательной к графику функции применяется представление «абсцисса точки касания». Данная величина может задаваться первоначально в условиях задачи либо же ее нужно определять самосильно.

Инструкция

1. Начертите на листе в клеточку оси координат х и у. Изучите заданное уравнение для графика функции. Если оно является линейным, то довольно узнать два значения для параметра у при всяких х, позже чего возвести обнаруженные точки на оси координат и объединить их прямой линией. Если же график нелинейный, то составьте таблицу зависимости у от х и подберите как минимум пять точек для построения графика.

2. Постройте график функции и поставьте на оси координат заданную точку касательной. Если она совпадает с функцией, то ее координата х приравнивается к букве «а», которой обозначается абсцисса точки касания.

3. Определите значение абсциссы точки касания для случая, когда заданная точка касательной не совпадает с графиком функции. Задаем 3-й параметр буквой «а».

4. Запишите уравнение функции f(a). Для этого в начальное уравнение взамен х подставьте а. Обнаружьте производную функции f(x) и f(a). Подставьте нужные данные в всеобщее уравнение касательной, которое имеет вид: y = f(a) + f ‘(a)(x – a). В итоге получить уравнение, которое состоит из 3 незнакомых параметров.

5. Подставьте в него взамен х и у координаты заданной точки, через которую проходит касательная. Позже этого обнаружьте решение полученного уравнения для всех а. Если оно является квадратным, то будет два значения абсциссы точки касания. Это значит, что касательная проходит два раза вблизи графика функции.

6. Нарисуйте график заданной функции и параллельной прямой, которые заданы по условию задачи. В этом случае нужно также задать неведомый параметр а и подставить его в уравнение f(a). Приравняйте производную f(a) к производной уравнения параллельной прямой. Данное действие выходит из данные параллельности 2-х функций. Обнаружьте корни полученного уравнения, которые будут являться абсциссами точки касания.

Совет 5: Как обнаружить угловой показатель касательной

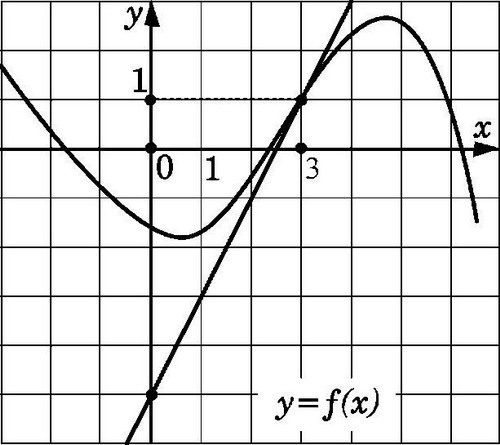
Прямая y=f(x) будет касательной к изображенному на рисунке графику в точке х0 в том случае, если она проходит через точку с координатами (х0; f(x0)) и владеет угловым показателем f'(x0). Обнаружить такой показатель, зная особенности касательной, нетрудно.



Вам понадобится

• – математический справочник;
• – легкой карандаш;
• – тетрадь;
• – транспортир;
• – циркуль;
• – ручка.

Инструкция

1. Обратите внимание на то, что график дифференцируемой в точке х0 функции f(x) ничем не отличается от отрезка касательной. Ввиду этого, он довольно близок к отрезку l, тот, что проходит через точки (х0; f(х0)) и (х0+?x; f(x0 + ?x)). Для того дабы задать прямую, которая проходит через некую точку А с показателями (х0; f(х0)), следует указать ее угловой показатель. При этом угловой показатель равен ?y/?x секущей касательной (?х?0) и тяготится к числу f‘(x0).

2. Если значения f‘(x0) не существует, то либо касательной нет, либо она проходит вертикально. Ввиду этого, присутствие производной функции в точке х0 обусловлено существованием невертикальной касательной, соприкасающейся с графиком функции в точке (х0, f(х0)). В этом случае угловой показатель касательной равен будет f'(х0). Таким образом, становится ясен геометрический толк производной – расчет углового показателя касательной.

3. Изобразите на рисунке добавочные касательные, которые бы соприкасались с графиком функции в точках x1, х2 и х3, а также подметьте углы, образуемые этими касательными с осью абсцисс (такой угол отсчитывают в правильном направлении от оси до касательной прямой). К примеру, 1-й угол, то есть, ?1, будет острым, 2-й (?2) – тупой, а 3-й (?3) равен нулю, от того что проведенная касательная прямая параллельна оси ОХ. В таком случае тангенс тупого угла – негативное значение, тангенс острого угла – позитивное, а при tg0 итог равен нулю.

Обратите внимание!
Верно определите угол, образуемый касательной. Для этого используйте транспортир.

Полезный совет
Две наклонные прямые будут параллельными в том случае, если их угловые показатели равны между собой; перпендикулярными, если произведение угловых показателей этих касательных равно -1.

Совет 6: Как обнаружить координаты точки касания

Раньше чем приступить к нахождению координат точки касания, нужно проверить вероятность проведения касательной. Для этого исполните обзор функции, описывающей заданную кривую на определенном участке.

Инструкция

1. Касательная к произвольной линии на плоскости в прямоугольной системе координат — это предел, к которому тяготится секущая к данной косой при максимальном сближении точек пересечения косой и прямой.

2. Следственно, касательная имеет только одну всеобщую точку с косой. Впрочем это заявление объективно для сурово определенного участка. В зависимости от поведения косой в иных областях координатной плоскости, касательная может пересекать заданную линию либо, напротив, удаляться от нее.

3. К некоторым кривым дозволено провести касательную в всякий точке. Примеры таких линий — окружность, эллипс. Другие постоянные кривые могут иметь точки, в которых возвести касательную нереально. Это происходит на участках, где секущая не тяготится к одному предельному расположению.

4. Пускай произвольная кривая описывается выражением Y=F(x). Всеобщий вид уравнения прямой Y=kx+a. Видимо, что в точке касания с координатами (Xo, Yо) объективно равенство: F(Xo)=kXo+a.

5. Если функция F(x) дифференцируема в точке Xo, в этой точке дозволено провести касательную к косой, и показатель наклона касательной к оси OX равен значению производной функции: k=F'(Xo). Уравнение касательной в точке касания принимает вид Yo=F'(Xo)*Xo+a. Задача нахождения координат точки касания сводится к решению системы 2-х уравнений с двумя неведомыми Yo=F(Xo) и Yo= F'(Xo)*Xo+a.

6. Плоскость является касательной к поверхности, если имеет всеобщую с поверхностью точку и прямую либо плоскую кривую линию. Определение координат (Xo Yo Zo) всеобщей точки касательной плоскости и заданной криволинейной поверхности Z=F(x,y) допустимо в случае если функция F(x,y) имеет полный дифференциал в данной точке.

Видео по теме

Совет 7: Как решать график функции и касательной

Задача составления уравнения касательной к графику функции сводится к необходимости совершения отбора из множества прямых тем, которые могут удовлетворить заданным требованиям. Все этим прямые могут задаваться либо точками, либо угловым показателем. Для того дабы решить график функции и касательной, нужно исполнить определенные действия.

Инструкция

1. Прочитайте наблюдательно задачу по составлению уравнения касательной. Как водится, имеется определенное уравнение графика функции , выраженное через x и y, а также координаты одной из точек касательной.

2. Постройте график функции в координатах осей x и y. Для этого нужно составить таблицу соотношения равенства y при заданном значении x. Если график функции нелинейный, то для ее построения потребуется, как минимум, пять значений координат. Начертите оси координат и график функции . Поставьте также точку, которая указана в условии задачи.

3. Обнаружьте значение абсциссы точки касания, которую обозначаются буквой «а». Если она совпадает с заданной точкой касательной, то «а» будет равно ее х-координате. Определите значение функции f(a), подставив в уравнение функции величину абсциссы.

4. Определите первую производную уравнения функции f’(x) и подставьте в него значение точки «а».

5. Возьмите всеобщее уравнение касательной, которое определяется как y = f(a) = f (a)(x – a), и подставьте в него обнаруженные значения a, f(a), f ‘(a). В итоге будет обнаружено решение графика функций и касательной.

6. Решите задачу другим методом, если заданная точка касательной не совпала с точкой касания. В этом случае нужно в уравнение касательной взамен цифр подставить букву «а». Позже этого взамен букв «х» и «у» подставьте значение координат заданной точки. Решите получившееся уравнение, в котором буква «а» является незнакомой. Поставьте полученное значение в уравнение касательной.

7. Составьте уравнение касательной с буквой «а», если в условии задачи задано уравнение функции и уравнение параллельной линии касательно желанной касательной. Позже этого нужно обнаружить производную функции параллельной прямой, дабы определить координату у точки «а». Подставьте соответствующее значение в уравнение касательной и решите функцию.

Совет 8: Как обнаружить тангенс угла наклона касательной

Геометрический толк производной первого порядка функции F(х) представляет собой касательную прямую к ее графику, проходящую через заданную точку косой и совпадающую с ней в этой точке. Причем значение производной в данной точке х0 является угловым показателем либо напротив – тангенсом угла наклона касательной прямой k = tg a = F`(х0). Вычисление данного показателя – одна из особенно распространенных задач теории функций.

Инструкция

1. Запишите заданную функцию F(x), скажем F(x) = (x? + 15х +26). Если в задаче очевидно указана точка, через которую проводится касательная, скажем, ее координата х0 = -2, дозволено обойтись без построения графика функции и дополнительных прямых на декартовой системе ОХY. Обнаружьте производную первого порядка от заданной функции F`(x). В рассматриваемом примере F`(x) = (3x? + 15). Подставьте заданное значение довода х0 в производную функции и вычислите ее значение: F`(-2) = (3(-2)? + 15) = 27. Таким образом, вы обнаружили tg a = 27.

2. При рассмотрении задачи, где требуется определить тангенс угла наклона касательной к графику функции в точке пересечения этого графика с осью абсцисс, вам потребуется вначале обнаружить числовое значение координат точки пересечения функции с ОХ. Для наглядности отменнее каждого исполнить построение графика функции на двухмерной плоскости ОХY.

3. Задайте координатный ряд для абсцисс, скажем, от -5 до 5 с шагом 1. Подставляя в функцию значения х, вычислите соответствующие им ординаты у и отложите на координатной плоскости полученные точки (х, у). Объедините точки плавной линией. Вы увидите на исполненном графике место пересечения функцией оси абсцисс. Ордината функции в данной точке равна нулю. Обнаружьте численное значение соответствующего ей довода. Для этого заданную функцию, скажем F(x) = (4x? – 16), приравняйте к нулю. Решите полученное уравнение с одной переменной и вычислите х: 4x? – 16 = 0, x? = 4, х = 2. Таким образом, согласно условию задачи, тангенс угла наклона касательной к графику функции нужно обнаружить в точке с координатой х0 = 2.

4. Подобно описанному ранее методу определите производную функции: F`(x) = 8*x. После этого вычислите ее значение в точке с х0 = 2, что соответствует точке пересечения начальной функции с ОХ. Подставьте полученное значение в производную функции и вычислите тангенс угла наклона касательной: tg a = F`(2) = 16.

5. При нахождении углового показателя в точке пересечения графика функции с осью ординат (ОY) исполните схожие действия. Только координату желанной точки х0 сразу следует принять равной нулю.

Совет 9: Как обнаружить типичный вектор

Перед тем как ответить на поставленный вопрос, требуется определить, нормаль чего именно нужно искать. В данном случае, ориентировочно, в задаче рассматривается некая поверхность.

Инструкция

1. Приступая к решению поставленной задачи, следует помнить, что нормаль к поверхности определяется как нормаль к касательной плоскости. Исходя именно из этого и будет выбираться методология решения.

2. График функции 2-х переменных z=f(x, y)=z(x, y) – это поверхность в пространстве. Таким образом ее почаще каждого и задают. В первую очередь нужно обнаружить касательную плоскость к поверхности в некоторой точке М0(x0, y0, z0), где z0=z(x0, y0).

3. Для этого следует припомнить, что геометрический толк производной функции одного довода, это угловой показатель касательной к графику функции в точке, где y0=f(x0). Частные производные функции 2-х доводов находят, фиксируя «ненужный» довод верно так же, как и производные обыкновенных функций. Значит геометрический толк частной производной по x функции z=z(x, y) в точке (x0,y0) состоит в равенстве ее углового показателя касательной, к косой, образуемой пересечением поверхности и плоскости y=y0 (см. рис. 1).

4. Данные, отраженные на рис. 1, разрешают заключить, что уравнение касательной к поверхности z=z(x, y), содержащей точку М0(xo, y0, z0) в сечении при y=y0: m(x-x0)=(z-z0), y=y0. В каноническом виде дозволено записать:(x-x0)/(1/m)=(z-z0)/1, y=y0. Значит направляющий вектор этой касательной s1(1/m, 0, 1).

5. Сейчас, если угловой показатель касательно для частной производной по y обозначить n, то абсолютно видимо, что подобно предыдущему выражению, это приведет к (y-y0)/(1/n)=(z-z0), x=x0 и s2(0, 1/n, 1).

6. Дальше движение решения в виде поиска уравнения касательной плоскости дозволено перестать и перейти непринужденно к желанной нормали n. Ее дозволено получить как вектор ное произведение n=[s1, s2]. Вычислив его, будет определено, что в заданной точке поверхности (x0, y0, z0). n={-1/n, -1/m, 1/mn}.

7. Потому что всякий пропорциональный вектор также останется вектор ом нормали, комфортнее каждого результат представить в виде n={-n, -m, 1} и окончательно n(дz/дx, дz/дx, -1).

Видео по теме


Обратите внимание!
У незамкнутой поверхности имеется две стороны. В данном случае результат дан для «верхней» стороны, там где нормаль образует острый угол с осью 0Z.

Видео по теме