Совет 1: Как обнаружить углы равнобедренной трапеции

Трапеция – это плоская четырехугольная геометрическая фигура, отличительной спецификой которой является непременная параллельность одной пары несоприкасающихся сторон. Эти стороны именуются ее основаниями, а две непараллельные составляющие – боковыми сторонами. Разновидность трапеции, у которой длины боковых сторон идентичны, именуется равнобокой либо равнобедренной. Формулы нахождения углов такой трапеции легко вывести из свойств прямоугольного треугольника.

Инструкция

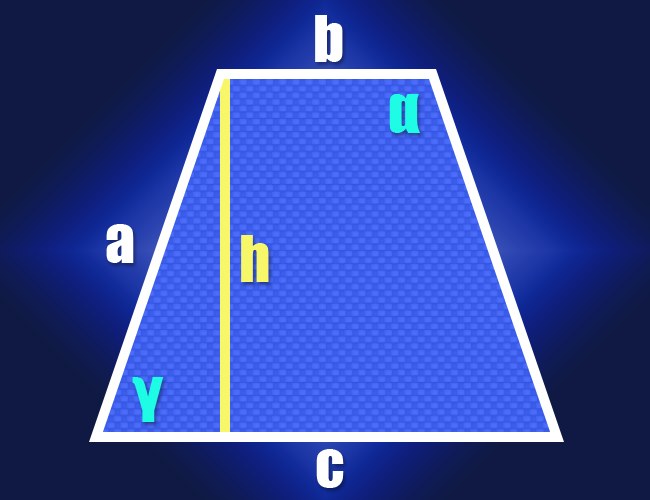
1. Если знамениты длины обоих оснований (b и c) и идентичных по определению боковых сторон (a) равнобедренной трапеции, то для вычисления величины одного из ее острых углов (?) дозволено применять свойства прямоугольного треугольника. Для этого опустите высоту из всякого прилегающего к короткому основанию угла. Прямоугольный треугольник будет образован высотой (катет), боковой стороной (гипотенуза) и отрезком длинного основания между высотой и ближней боковой стороной (2-й катет). Длину этого отрезка дозволено обнаружить, отняв от длины большего основания длину меньшего и поделив итог напополам: (c-b)/2.

2. Получив значения длин 2-х смежных сторон прямоугольного треугольника, переходите к вычислению угла между ними. Отношение длины гипотенузы (a) к длине катета ((c-b)/2) дает значение косинуса этого угла (cos(?)), а функция арккосинус поможет преобразовать его в величину угла в градусах: ?=arccos(2*a/(c-b)). Так вы получите величину одного из острых углов трапеции, а от того что она равнобедренна, то и 2-й острый угол будет иметь такую же величину. Сумма всех углов четырехугольника должна составлять 360°, а это значит, что сумма 2-х тупых углов будет равна разности между этим числом и удвоенной величиной острого угла. От того что оба тупых угла тоже будут идентичны, то для нахождения величины всего из них (?) эту разность нужно поделить напополам: ? = (360°-2*?)/2 = 180°-arccos(2*a/(c-b)). Сейчас у вас есть формулы вычисления всех углов равнобедренной трапеции по знаменитым длинам ее сторон.

3. Если длины боковых сторон фигуры неведомы, но дана ее высота (h), то делать надобно по такой же схеме. В этом случае в прямоугольном треугольнике, составленном из высоты, боковой стороны и короткого отрезка длинного основания, вам будут вестимы длины 2-х катетов. Их соотношение определяет тангенс надобного вам угла, а эта тригонометрическая функция тоже имеет своего антипода, преобразующего значение тангенса в величину угла – арктангенс. Полученные в предыдущем шаге формулы острого и тупого углов трансформируйте соответствующим образом: ?=arctg(2*h/(c-b)) и ? = 180°-arctg(2*h/(c-b)).

Совет 2: Как обнаружить углы четырёхугольника

Для решения этой задачи способами векторной алгебры, вам нужно знать следующие представления: геометрическая векторная сумма и скалярное произведение векторов, а также следует помнить качество суммы внутренних углов четырехугольника.



Вам понадобится

• – бумага;
• – ручка;
• – линейка.

Инструкция

1. Вектор – это направленный отрезок, то есть величина, считающаяся заданной всецело, если задана его длина и направление (угол) к заданной оси. Расположение вектора огромнее ничем не ограничено. Равными считаются два вектора, владеющие идентичными длинами и одним направлением. Следственно при применении координат векторы изображают радиус-векторами точек его конца (предисловие располагается в начале координат).

2. По определению: результирующим вектором геометрической суммы векторов именуется вектор, исходящий из начала первого и имеющего конец в конце второго, при условии, что конец первого, совмещен с началом второго. Это дозволено продолжать и дальше, строя цепочку подобно расположенных векторов. Изобразите данный четырехугольник ABCD векторами a, b, c и d в соответствии рис. 1. Видимо, что при таком расположении результирующий вектор d=a+ b+c.



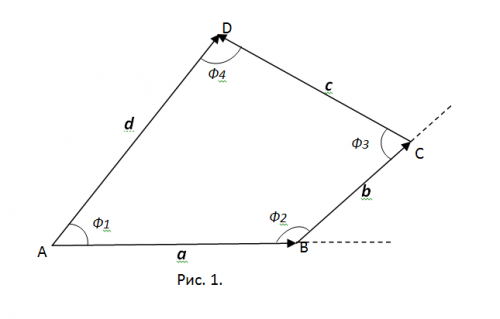
3. Скалярное произведение в данном случае комфортнее каждого определить на основе векторов a и d. Скалярное произведение, обозначаемое (a, d)= |a||d|cosф1. Тут ф1 – угол между векторами a и d. Скалярное произведение векторов, заданных координатами, определяется следующими выражением: (a(ax, ay), d(dx, dy))=axdx+aydy, |a|^2= ax^2+ ay^2, |d|^2= dx^2+ dy^2, тогда cos Ф1=(axdx+aydy)/(sqrt(ax^2+ ay^2)sqrt(dx^2+ dy^2)).

4. Основные представления векторной алгебры в привязке к поставленной задаче, приводят к тому, что для однозначной постановки этой задачи довольно задание 3 векторов, расположенных, возможен, на AB, BC, и CD, то есть a, b, c. Дозволено финально сразу задать координаты точек A, B, C, D, но данный метод является избыточным (4 параметра взамен 3-х).

5. Пример. Четырехугольник ABCD задан векторами его сторон AB, BC, CD a(1,0), b(1,1), c(-1,2). Обнаружить углы между его сторонами. Решение. В связи с высказанным выше, 4-й вектор (для AD) d(dx,dy)=a+ b+c={ax+bx +cx, ay+by+cy}={1,3}. Следуя методике вычисления угла между векторами аcosф1=(axdx+aydy)/(sqrt(ax^2+ ay^2)sqrt(dx^2+ dy^2))=1/sqrt(10), ф1=arcos(1/sqrt(10)).-cosф2=(axbx+ayby)/(sqrt(ax^2+ ay^2)sqrt(bx^2+ by^2))=1/sqrt2, ф2=arcos(-1/sqrt2), ф2=3п/4.-cosф3=(bxcx+bycy)/(sqrt(bx^2+ by^2)sqrt(cx^2+ cy^2))=1/(sqrt2sqrt5), ф3=arcos(-1/sqrt(10))=п-ф1. В соответствии с примечанием 2 – ф4=2п- ф1 – ф2- ф3=п/4.

Видео по теме


Обратите внимание!
Примечание 1. В определении скалярного произведения применяется угол между векторами. Тут, скажем, ф2 – это угол между АВ и ВС, а между a и b данный угол п-ф2. сos(п- ф2)=- сosф2. Подобно для ф3.Примечание 2. Вестимо, что сумма углов четырехугольника равна 2п. Следственно ф4=2п- ф1 – ф2- ф3.