Совет 1: Как обнаружить центр окружности
Часто столярам и плотникам в работе требуется геометрия. Один из самых блестящих примеров – построение верной окружности. Еще одна задача, с которой в данном случае дозволено столкнуться – это определение центра круга, не прибегая к особым инструментам и трудным вычислениям.
Вам понадобится
- Линейка и карандаш
Инструкция
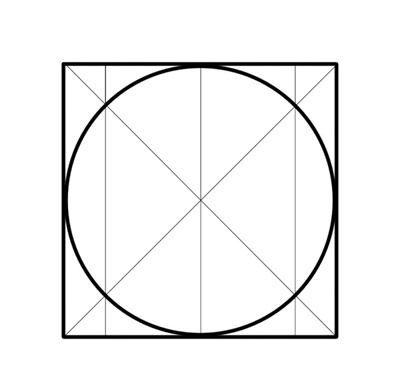
1. Для того дабы обнаружить центр окружности, нужно вначале вписать ее в квадрат. То есть все стороны четырехугольника обязаны касаться круга. Для этого проведите с подмогой линейки четыре ровные линии.
2. Сейчас объедините по диагонали два противоположных угла. Следите за тем, дабы линия разбивала угол квадрата на две равные части. Объедините прямыми все 4 угла квадрата.
3. Точка пересечения данных прямых и будет центром окружности.
4. Еще одной фигурой, которая может подмогнуть определить центр круга, является прямоугольный треугольник. Его также надобно вписать в окружность. А после этого поделить противоположную прямому углу сторону напополам. Середина гипотенузы и будет центром окружности.
Совет 2: Как поделить круг на равные части
В силу определенных причин изредка надобно поделить круг на равные части, но не неизменно имеются нужные навыки и знания, дабы это осуществить. А чай сделать это дозволено различными методами, всякий из которых по-своему практичен и комфортен.

Вам понадобится
- Бумага, линейка, транспортир, карандаш, ножницы.
Инструкция
1. Дозволено пойти особенно простым путем, то есть сделать копию надобной фигуры, вырезать ее и после этого путем сгибания поделить на нужное число секций. Впрочем тут необходимо рассматривать, что таким образом, складывая круг напополам, дозволено его поделить на 2 части. Сложив фигуру еще раз, получим 4 части. Продолжая складывать круг , в итоге будет 8, а после этого 16 частей. После этого дозволено приложить вырезанный круг к основному и подметить в местах заломов секции на стержневой требуемой фигуре.
2. Впрочем при делении круг а таким методом не получается 3, 5, 7, 9 либо 11 частей. В этих случаях придется воспользоваться транспортиром. Если нет вероятности определить середину круг а, то вновь вначале надобно обвести фигуру, вырезать ее и сложить в два, а после этого в четыре раза. Перпендикулярные линии на пересечении дадут точку, которая показывает середину. От нее нужно проводить все отметки.
3. Каждый круг составляет 360°, следственно, дозволено посчитать градусы всякого числа частей. Скажем, надобно сделать 5 секций. Для этого 360° поделите на 5 частей – получается 72°. То есть, всякий секция будет составлять 72°. Поставьте транспортир, тот, что охватывает 180° на середину и отмерьте 72°. Проведите линию от центральной серединной точки до отмеренного градуса, после этого исполните то же самое еще 3 раза. В результате получится 5 равных частей круг а.
4. Если нужно поделить круг , скажем, на 12 частей, то для этого путем складывания рабочего круг а, поделите его на 4 части. На центральную точку положите транспортир. Если 360° поделить на 12, получится 30°. То есть каждого будет 12 частей по 30°. Таким образом, вследствие транспортиру дозволено поделить круг дословно на всякое число равных частей.
Совет 3: Как обнаружить центр фигуры
Центр фигуры дозволено обнаружить несколькими методами, смотря какие данные о ней теснее вестимы. Стоит разобрать нахождение центра окружности, которая является общностью точек, располагающихся на равном расстоянии от центра, потому что эта фигура – одна из особенно распространенных.

Вам понадобится
- – угольник;
- – линейка.
Инструкция
1. Примитивный метод обнаружить центр окружности – согнуть лист бумаги, на котором она начерчена, удостоверясь, глядя на просвет, что она сложилась верно напополам. После этого согните лист перпендикулярно первому сгибу. Так вы получите диаметры, точка пересечения которых и есть центр фигуры.
2. Финально, данный метод совершенен, только если окружность начерчена на бумаге, довольно тонкой, дабы дозволено было посмотреть на просвет, верно ли труден лист.
3. Возможен, рассматриваемую фигуру начертили на твердой, несгибаемой поверхности либо это отдельная деталь, которая также не поддается сгибу. Дабы обнаружить центр окружности в этом случае, вам надобна линейка.
4. Диаметр является самым длинным отрезком, соединяющим 2 точки окружности. Как вестимо, проходит он через центр, следственно задача нахождения центра окружности сводится к нахождению диаметра и его середины.
5. Наложите линейку на окружность, позже чего зафиксируйте в всякий точке фигуры нулевую отметку. Приложите линейку к окружности, получив секущую, а после этого двигайте по направлению к центру фигуры. Длина секущей будет вырастать, пока не дойдет до пиковой точки. Вы получите диаметр, а обнаружив его середину, обнаружите и центр окружности.
6. Центр описанной окружности для всякого треугольника располагается на пересечении срединных перпендикуляров. В случае, если треугольник прямоугольный, ее центр неизменно будет совпадать с серединой гипотенузы. То есть решение кроется в построении внутри окружности прямоугольного треугольника с вершинами, лежащими на окружности.
7. Трафаретом для прямого угла могут послужить школьный либо строительный угольник, линейка либо даже лист бумаги/картона. Разместите в всякую точку окружности вершину прямого угла, сделайте отметки в тех местах, где стороны угла пересекают рубеж окружности, объедините их. У вас получился диаметр – гипотенуза.
8. Таким же методом обнаружьте еще один диаметр, место пересечения 2-х таких отрезков и будет центром окружности.
Видео по теме
Обратите внимание!
Квадрат, вблизи которого описана окружность, должен быть построен по правилам. Нужно, дабы все стороны четырехугольника были равны, а радиус углов составлял 90 градусов.









