Совет 1: Как обнаружить синус угла в равнобедренном треугольнике

Равнобедренным треугольником именуется выпуклая геометрическая фигура из 3 вершин и 3 соединяющих их отрезков, два из которых имеют идентичную длину. А синус – это тригонометрическая функция, которую дозволено применять для численного выражения зависимости между соотношением длин сторон и величинами углов во всех треугольниках, включая и равнобедренные.

Инструкция

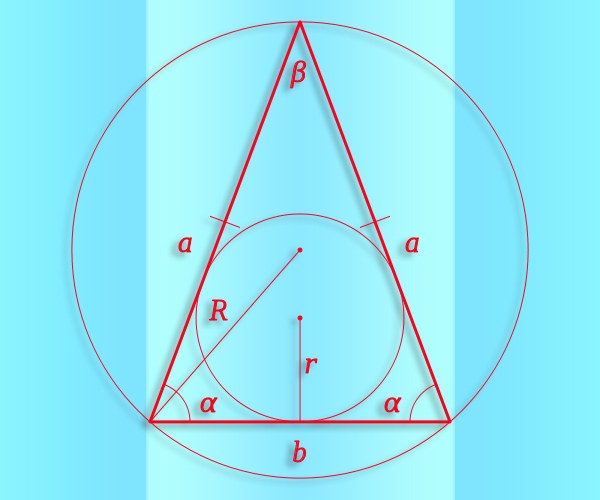
1. Если из начальных данных вестима величина правда бы одного угла (?) в равнобедренном треугольнике, это дозволит обнаружить и два других (? и ?), а значит и синус всякого из них. Исходите из теоремы о сумме углов, которая заявляет, что в треугольнике она неукоснительно должна быть равна 180°. Если угол знаменитой величины лежит между боковыми сторонами, величина всякого из 2-х других равна половине разности между 180° и вестимым углом. Значит, вы можете применять в расчетах такое тождество: sin(?) = sin(?) = sin((180°-?)/2). Если же вестимый угол примыкает к основанию треугольника, это тождество распадется на два равенства: sin(?) = sin(?) и sin(?) = sin(180°-2*?).

2. Зная радиус (R) окружности, описанной около такого треугольника, и длину всякий из сторон (скажем, а) дозволено не прибегая к вычислению тригонометрических функций рассчитать синус угла (?), лежащего наоборот этой стороны. Используйте для этого теорему синус ов – из нее вытекает, что необходимая вам величина равна половине соотношения между длиной стороны и радиусом: sin(?) = ?*R/a.

3. Знаменитые площадь (S) и длина боковой стороны (а) равнобедренного треугольника дозволят рассчитать синус угла (?), лежащего наоборот основания фигуры. Для этого удвойте площадь и поделите итог на возведенную в квадрат длину боковой стороны: sin(?) = 2*S/a?. Если помимо длины боковой стороны вестима и длина основания (b), квадрат дозволено заменить произведением длин этих 2-х сторон: sin(?) = 2*S/(a*b).

4. Если вестимы длины боковой стороны (а) и основания (b) равнобедренного треугольника, для вычисления синус а угла при основании (?) дозволено задействовать даже теорему косинус ов. Из нее вытекает, что косинус этого угла равен половине отношения длины основания к длине боковой стороны: cos(?) = ?*b/a. Синус и косинус связаны таким равенством: sin?(?) = 1-cos?(?). Следственно для вычисления синус а извлеките квадратный корень из разницы между единицей и четвертью соотношения квадратов длин основания и боковой стороны: sin(?) = ?(1-cos2(?)) = ?(1-?*b?/а?).

Совет 2: Как обнаружить высоту в равнобедренном треугольнике

У равнобедренного треугольника две стороны равны, углы при его основании тоже равны. Следственно высоты, проведенные к боковым сторонам, будут равны друг другу. Высота, проведенная к основанию равнобедренного треугольника, будет единовременно медианой и биссектрисой этого треугольника.

Инструкция

1. Пускай высота AE проведена к основанию BC равнобедренного треугольника ABC. Треугольник AEB будет прямоугольным, потому что AE – высота. Боковая сторона AB будет гипотенузой этого треугольника, а BE и AE – его катетами.По теореме Пифагора (AB^2) = (BE^2)+(AE^2). Тогда (BE^2) = sqrt((AB^2)-(AE^2)). Потому что AE единовременно и медиана треугольника ABC, то BE = BC/2. Следственно, (BE^2) = sqrt((AB^2)-((BC^2)/4)).Если задан угол при основании ABC, то из прямоугольного треугольника высота AE равна AE = AB/sin(ABC). Угол BAE = BAC/2, потому что AE – биссектриса треугольника. Отсель, AE = AB/cos(BAC/2).

2. Пускай сейчас проведена высота BK к боковой стороне AC. Эта высота теснее не является ни медианой, ни биссектрисой треугольника. Для вычисления ее длины существует всеобщая формула.Пускай S – площадь этого треугольника. Сторону AC, на которую опущена высота, дозволено обозначить за b. Тогда из формулы площади треугольника будет находиться длина высоту BK: BK = 2S/b.

3. Из этой формулы видно, что высота, проведенная к стороне с (AB), будет иметь такую же длину, потому что b = c = AB = AC.

Совет 3: Как обнаружить угол в равнобедренном треугольнике

Под равнобедренным треугольником подразумевается такой треугольник, у которого равны между собой 2 стороны, а третья, в свою очередь, именуется основанием равнобедренного треугольника. Для подсчета размеров углов в данном треугольнике существует несколько методов.



Вам понадобится

• Стороны равнобедренного треугольника, один из углов, радиус описанной вокруг треугольника окружности.

Инструкция

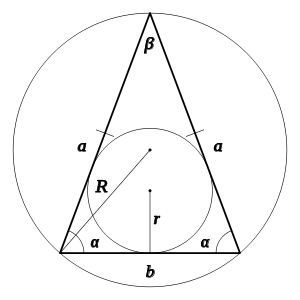
1. Возможен, дан равнобедренный треугольник, в котором угол ? – угол при основании равнобедренного треугольника, а ? – противолежащий основанию угол. Тогда, зная один из указанных углов, дозволено рассчитать незнакомый:? = (? – ?)/2;? = ? – 2*?. ? – это константа, ее размер принято считать равной 3.14.

2. Если вокруг равнобедренного треугольника с равными сторонами a, основанием b описать окружность радиуса R, то углы ? и ? дозволено будет рассчитать так:? = arcsin(a/2R);? = arcsin(b/2R)

Совет 4: Как обнаружить длину стороны в равнобедренном треугольнике

Равнобедренным именуется треугольник, в котором длины 2-х его сторон идентичны. Дабы вычислить размер какой-нибудь из сторон нужно знать длину иной стороны и один из углов либо радиус описанной вокруг треугольника окружности. В зависимости от вестимых величин, для расчетов нужно применять формулы, вытекающие из теорем синуса либо косинуса, либо из теоремы о проекциях.

Инструкция

1. Если вестима длина основания равнобедренного треугольника (A) и величина прилежащего к нему угла (угла между основанием и всякий боковой стороной) (α), то вычислить длину всякой из боковых сторон (B) дозволено исходя из теоремы косинусов. Она будет равна частному от деления длины основания на удвоенное значение косинуса вестимого угла B=A/(2*cos(α)).

2. Длину стороны равнобедренного треугольника, являющейся его основанием (A), дозволено вычислить исходя из той же теоремы косинусов, если знамениты длина его боковой стороны (B) и угол между ней и основанием (α). Она будет равна удвоенному произведению вестимой стороны на косинус знаменитого угла A=2*B*cos(α).

3. Иной метод нахождения длины основания равнобедренного треугольника дозволено применять, если вестима величина противолежащего ему угла (β) и длина боковой стороны (B) треугольника. Она будет равна удвоенному произведению длины боковой стороны на синус половины величины знаменитого угла A=2*B*sin(β /2).

4. Подобно дозволено вывести и формулу вычисления боковой стороны равнобедренного треугольника. Если вестима длина основания (A) и величина угла между равными сторонами (β), то длина всей из них (B) будет равна частному от деления длины основания на удвоенный синус половины величины знаменитого угла B=A/(2*sin(β /2)).

5. Если вестим радиус описанной вокруг равнобедренного треугольника окружности (R), то длины его сторон дозволено рассчитать, зная величину одного из углов. Если вестима величина угла между боковыми сторонами (β), то длина стороны , являющейся основанием (A), будет равна удвоенному произведению радиуса описанной окружности на синус этого угла A=2*R*sin(β).

6. Если знамениты радиус описанной окружности (R) и величина угла, прилегающего к основанию (α), то длина боковой стороны (B) будет равна удвоенному произведению длины основания на синус знаменитого угла B=2*R*sin(α).

Совет 5: Что такое синус

На прямоугольном треугольнике, как наипростейшем из многоугольников, различные ученые супруги оттачивали свои познания в области тригонометрии еще в те времена, когда эту область математики никто даже не называл таким словом. Следственно указать автора, выявившего обоснованности в соотношениях длин сторон и величин углов в этой плоской геометрической фигуре, сегодня не представляется допустимым. Такие соотношения названы тригонометрическими функциями и поделены на несколько групп, стержневой из которых условно считаются «прямые» функции. К этой группе отнесены каждого две функции и одна из них – синус.

Инструкция

1. По определению в прямоугольном треугольнике один из углов равен 90°, а в силу того, что сумма его углов в евклидовой геометрии обязана быть равной 180°, два других угла являются острыми (т.е. поменьше 90°). Обоснованности соотношений именно этих углов и длин сторон и описывают тригонометрические функции.

2. Функция, называемая синусом острого угла, определяет соотношение между длиной 2-х сторон прямоугольного треугольника, одна из которых лежит наоборот этого острого угла, а иная примыкает к нему и лежит наоборот прямого угла. Потому что сторона, лежащая наоборот прямого угла в таком треугольнике, именуется гипотенузой, а две другие – катетами, то определение функции синус дозволено сформулировать как соотношение между длинами противолежащего катета и гипотенузы.

3. Помимо такого простейшего определения этой тригонометрической функции сегодня существуют и больше трудные: через окружность в декартовых координатах, через ряды, через решения дифференциальных и функциональных уравнений. Эта функция постоянна, то есть ее доводами («областью определений») может быть всякое число – от безгранично негативного до безгранично правильного. А максимум и минимум значений этой функции ограничены диапазоном от -1 до +1 – это «область ее значений». Минимальное значение синус принимает при угле в 270°, что соответствует 3/2 числа Пи, а наивысшее получается при 90° (? от Пи). Нулевыми значения функции становятся при 0°, 180°, 360° и т.д. Из каждого этого вытекает, что синус является функцией периодической и период ее равен 360° либо удвоенному числу Пи.

4. Для фактических расчетов значений этой функции от заданного довода дозволено применять калькулятор – безусловное множество из них (включая программный калькулятор, встроенный в операционную систему вашего компьютера) имеет соответствующую опцию.

Видео по теме

Совет 6: Как обнаружить синус угла между векторами

Вектор в многомерном евклидовом пространстве задается координатами своей исходной точки и точки, определяющей его величину и направление. Отличие между направлениями 2-х таких векторов определяется величиной угла. Зачастую в различного рода задачах из области физики и математики предлагается обнаружить не сам данный угол, а величину производной от него тригонометрической функции – синуса.

Инструкция

1. Используйте для определения синуса угла между двумя векторами вестимые формулы скалярного умножения векторов. Таких формул существует, как минимум, две. В одной из них в качестве переменной задействован косинус надобного угла , узнав тот, что вы сумеете вычислить и синус.

2. Составьте равенство и вычлените из него косинус. По одной формуле скалярное произведение векторов равно их длинам, перемноженным друг на другу и на косинус угла , а по иной – сумме произведений координат по всей из осей. Приравняв обе формулы дозволено сделать итог, что косинус угла должен быть равен отношению суммы произведений координат к произведению длин векторов.

3. Запишите полученное равенство. Для этого нужно обозначить координаты обоих векторов. Возможен, они даны в трехмерной декартовой системе и их исходные точки перенесены в предисловие координатной сетки. Направление и величина первого вектора будет задана точкой (X?,Y?,Z?), второго – (X?,Y?,Z?), а угол обозначьте буквой ?. Тогда длины всякого из векторов дозволено высчитать, скажем, по теореме Пифагора для треугольников, образуемых их проекциями на всякую из координатных осей: ?(X?? + Y?? + Z??) и ?(X?? + Y?? + Z??). Подставьте эти выражения в сформулированную на предыдущем шаге формулу и вы получите такое равенство: cos(?) = (X?*X? + Y?*Y? + Z?*Z?) / (?(X?? + Y?? + Z??) * ?( X?? + Y?? + Z??)).

4. Используйте тот факт, что сумма возведенных в квадрат значений синуса и косинуса от угла одной величины неизменно дает единицу. Значит, построив полученное на предыдущем шаге выражение для косинуса в квадрат и отняв от единицы, а после этого обнаружь квадратный корень, вы решите задачу. Запишите надобную формулу в всеобщем виде: sin(?) = ?(1-cos(?)?) = ?(1 – ((X?*X? + Y?*Y? + Z?*Z?) / (?(X?? + Y?? + Z??) * ?( X?? + Y?? + Z??))?) = ?(1 – ((X?*X? + Y?*Y? + Z?*Z?)? / ((X?? + Y?? + Z??) * ( X?? + Y?? + Z??))).

Видео по теме

Совет 7: Как обнаружить длину высоты в равнобедренном треугольнике

Высотами в треугольнике называют три отрезка прямых, всякий из которых перпендикулярен одной из сторон и соединяет ее с противолежащей вершиной. Как минимум две стороны и два угла в равнобедренном треугольнике имеют идентичные величины, следственно и длины 2-х высот обязаны быть равны. Это обстоятельство гораздо упрощает вычисление длин высот фигуры.

Инструкция

1. Высоту (Hc), проведенную к основанию равнобедренного треугольника, дозволено рассчитать, зная длины этого основания (c) и боковой стороны (a). Для этого дозволено применять теорему Пифагора, потому что высота, боковая сторона и половина основания образуют прямоугольный треугольник. Высота и половина основания в нем являются катетами, следственно для решения задачи извлеките корень из разности между возведенной в квадрат длиной боковой стороны и четвертью квадрата длины основания: Hс = ?(a?-?*c?).

2. Эту же высоту (Hc) дозволено вычислить и по длине всякий из сторон, если в условиях приведена величина правда бы одного угла. Если это угол при основании треугольника (?) а вестимая длина определяет величину боковой стороны (a), для приобретения итоге перемножьте длину знаменитой стороны и синус знаменитого угла: Hс = a*sin(?). Эта формула вытекает из теоремы синусов.

3. Если вестима длина основания (с) и величина прилегающего к нему угла (?), для вычисления высоты (Hc), половину длины основания умножьте на синус знаменитого угла и поделите на синус разницы между 90° и величиной того же угла: Hс = ?*c*sin(?)/sin(90°-?).

4. При знаменитых размерах основания (с) и противолежащего ему угла (?) для вычисления высоты (Hc) умножайте половину длины вестимой стороны на синус разницы между 90° и половиной вестимого угла, а итог разделяете на синус половины того же угла: Hс = ?*c*sin(90°-?/2)/sin(?/2). Эта формула, как и две предыдущие, вытекает из теоремы синусов в сочетании с теоремой о сумме углов в треугольнике .

5. Длину высоты, проведенной к одной из боковых сторон (Ha) дозволено вычислить, скажем, зная длину этой стороны (a) и площадь равнобедренного треугольника (S). Дабы это сделать, обнаружьте удвоенную величину соотношения между площадью и длиной знаменитой стороны: Ha = 2*S/a.

Совет 8: Как обнаружить синус, зная угол

Одной из фундаментальных основ точных наук является представление о тригонометрических функциях. Они определяют примитивные отношения между сторонами прямоугольного треугольника. К семейству данных функций относится синус. Обнаружить его, зная угол, дозволено огромным числом методов, включающих экспериментальные, вычислительные способы, а также применение справочной информации.



Вам понадобится

• – калькулятор;
• – компьютер;
• – электронные таблицы;
• – таблицы брадиса;
• – бумага;
• – карандаш.

Инструкция

1. Используйте калькулятор с функцией вычисления синуса для приобретения необходимых значений на основании познания угла. Сходственный функционал сегодня имеют даже самые примитивные устройства. При этом вычисления производятся с дюже высокой степенью точности (как водится, до восьми и больше знаков позже запятой).

2. Примените программное обеспечение, представляющее собой среду для работы с электронными таблицами, запущенное на персональном компьютере. Примерами сходственных приложений являются Microsoft Office Excel и OpenOffice.org Calc. Введите в всякую ячейку формулу, состоящую из вызова функции вычисления синуса с надобным доводом. Нажмите Enter. В ячейке отобразится желанная величина. Превосходством электронных таблиц является вероятность стремительного расчета значений функций для большого комплекта доводов.

3. Узнайте приближенное значение синуса угла из таблиц Брадиса, если они имеются в наличии. Их недостатком является точность значений, ограниченная четырьмя знаками позже запятой.

4. Обнаружьте приближенное значение синуса угла, совершив геометрические построения. На листе бумаги вычертите отрезок. При помощи транспортира отложите от него угол, синус которого нужно обнаружить. Начертите еще один отрезок, пересекающий 1-й в некоторой точке. Перпендикулярно первому же отрезку проведите прямую линию, пересекающую два теснее существующих отрезка. Получится прямоугольный треугольник. Измерьте длину его гипотенузы и катета, противолежащего углу, построенному при помощи транспортира. Поделите второе значение на первое. Это и будет желанная величина.

5. Рассчитайте синус угла, применяя разложение в ряд Тейлора. Если значение угла представлено в градусах, переведите его в радианы. Используйте формулу вида: sin(х) = х – (х^3)/3! + (х^5)/5! – (х^7)/7! + (х^9)/9! – … Для возрастания скорости расчетов записывайте нынешнее значение числителя и знаменателя последнего члена ряда, производя вычисление дальнейшего значения на основе предыдущего. Увеличивайте длину ряда для приобретения больше точной величины.

Видео по теме