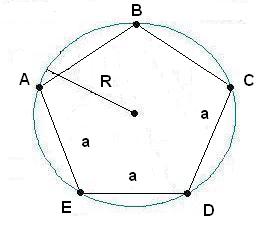
Совет 1: Как обнаружить радиус вписанной окружности в равнобедренном треугольнике?

Зная стороны треугольника, дозволено обнаружить радиус вписанной в него окружности. Для этого применяется формула, дозволяющая обнаружить радиус, а после этого, длину окружности и площадь круга, а также другие параметры.

Инструкция

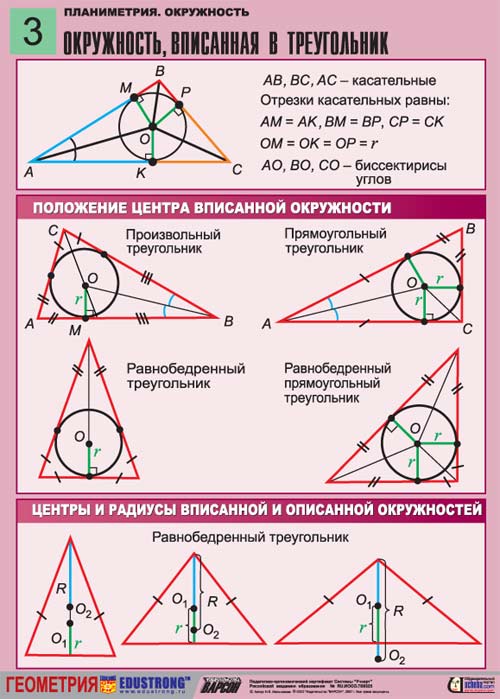
1. Представьте себе равнобедренный треугольник, в тот, что вписана окружность незнакомого радиуса R. От того что окружность является вписанной в треугольник, а не описанной вокруг него, все стороны этого треугольника являются касательными к ней. Высота, проведенная из вершины одного угла перпендикулярно к основанию, совпадает с медианой этого треугольника. Она проходит через радиус вписанной окружности.Следует подметить, что равнобедренным именуется тот треугольник, у которого две боковые стороны равны. Углы при основании этого треугольника обязаны быть тоже равны. Такой треугольник, единовременно, дозволено вписать в окружность и описать около нее.

2. Вначале обнаружьте неведомое основание треугольника. Для этого, как теснее сказано выше, проведите высоту из вершины треугольника к его основанию. Высота пересечет центр окружности. Если вестима правда бы одна из сторон треугольника, скажем, сторона CB, то вторая сторона ей равна, потому что треугольник является равнобедренным. В данном случае, это – сторона AC. Третью сторону, которая является основанием треугольника, обнаружьте по теореме Пифагора:c^2=a^2+a^2-2a^2*cosyУгол y между двумя равными сторонами обнаружьте исходя из того, что в равнобедренном треугольнике два угла равны. Соответственно, 3-й угол равен y=180-(a+b).

3. Обнаружив все три стороны треугольника, перейдите к решению задачи. Формула, объединяющая длины сторон и радиус, выглядит дальнейшим образом: r=(p-a)(p-b)(p-c)/p, где p=a+b+c/2 – сумма всех сторон, поделенных напополам, либо полупериметр.Если в окружность вписан равнобедренный треугольник, то в таком случае значительно легче находить радиус окружности. При умении радиуса окружности, дозволено обнаружить такие главные параметры, как площадь круга и длина окружности. Если в задании, напротив, дан радиус окружности – это является, в свою очередь, предпосылкой к нахождению сторон треугольника. Обнаружив стороны треугольника, дозволено вычислить его площадь и периметр. Эти вычисления обширно используются во многих инженерных задачах. Планиметрия – это базовая наука, по средствам которой постигают больше трудные геометрические вычисления.

Совет 2: Как обнаружить радиус описанной окружности

Окружность считается описанной вокруг многоугольника в том случае, если она касается всех его вершин. Что знаменательно, центр сходственной окружности совпадает с точкой пересечения перпендикуляров, проведенных из середин сторон многоугольника. Радиус описанной окружности всецело зависит от того многоугольника, вокруг которого она описана.



Вам понадобится

• Знать стороны многоугольника, его площадь/периметр.

Инструкция

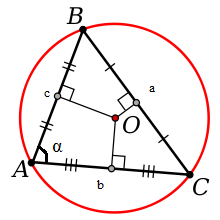
1. Подсчет радиуса описанной вокруг треугольника окружности .Если окружность описана вокруг треугольника со сторонами a, b, c, площадью S и углом ?, лежащим вопреки стороны a, то ее радиус R может быть рассчитан по дальнейшим формулам:1) R = (a*b*c)/4S;2) R = a/2sin?.



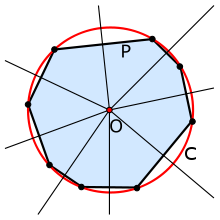
2. Подсчет радиуса окружности , описанной вокруг положительного многоугольника.Для расчета радиуса окружности , описанной вокруг положительного многоугольника, надобно воспользоваться дальнейшей формулой:R = a/(2 x sin (360 / (2 x n))), гдеa – сторона верного многоугольника;n – число его сторон.



Обратите внимание!
Вокруг многоугольника дозволено описать окружность только в том случае, если он положительный, т.е. все его стороны равны и все его углы равны.Принцип, гласящий, что центром описанной вокруг многоугольника окружности является пересечение его серединных перпендикуляров, объективен для всех верных многоугольников.

Совет 3: Как обнаружить высоту в равнобедренном треугольнике

У равнобедренного треугольника две стороны равны, углы при его основании тоже равны. Следственно высоты, проведенные к боковым сторонам, будут равны друг другу. Высота, проведенная к основанию равнобедренного треугольника, будет единовременно медианой и биссектрисой этого треугольника.

Инструкция

1. Пускай высота AE проведена к основанию BC равнобедренного треугольника ABC. Треугольник AEB будет прямоугольным, потому что AE – высота. Боковая сторона AB будет гипотенузой этого треугольника, а BE и AE – его катетами.По теореме Пифагора (AB^2) = (BE^2)+(AE^2). Тогда (BE^2) = sqrt((AB^2)-(AE^2)). Потому что AE единовременно и медиана треугольника ABC, то BE = BC/2. Следственно, (BE^2) = sqrt((AB^2)-((BC^2)/4)).Если задан угол при основании ABC, то из прямоугольного треугольника высота AE равна AE = AB/sin(ABC). Угол BAE = BAC/2, потому что AE – биссектриса треугольника. Отсель, AE = AB/cos(BAC/2).

2. Пускай сейчас проведена высота BK к боковой стороне AC. Эта высота теснее не является ни медианой, ни биссектрисой треугольника. Для вычисления ее длины существует всеобщая формула.Пускай S – площадь этого треугольника. Сторону AC, на которую опущена высота, дозволено обозначить за b. Тогда из формулы площади треугольника будет находиться длина высоту BK: BK = 2S/b.

3. Из этой формулы видно, что высота, проведенная к стороне с (AB), будет иметь такую же длину, потому что b = c = AB = AC.

Совет 4: Как обнаружить длину окружности круга

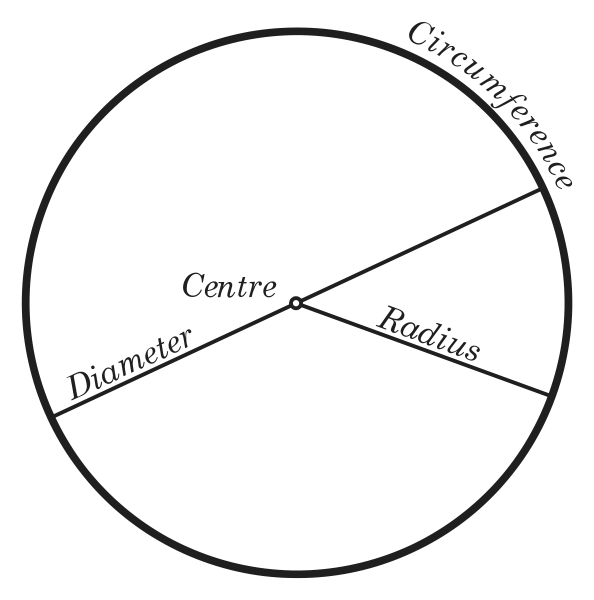
У такой геометрической фигуры, как окружность, имеется несколько колляций: радиус, диаметр, площадь, длина окружности . Все они взаимосвязаны между собой. Это обозначает, что в всякий из них заключено довольно информации для определения всех остальных колляций того же круга .

Инструкция

1. Окружность представляет собой кривую, ограничивающую плоскость, называемую кругом. Иными словами, окружностью именуется геометрическое место точек плоскости, равноудаленных от ее центра. Отрезки объединенные с центром, окружности именуются ее радиусами, а расстояние от одной точки до иной, проходящее через центр, именуется диаметром окружности . Диаметр окружности равен двум радиусам: D=2r. Уравнение окружности в аналитической геометрии имеет вид:x^2+y^2=R^2Существует также представление хорды окружности . Она тоже получается путем соединения 2-х точек окружности , но не непременно проходит через ее центр. Все диаметры, которые проходят через середину хорды, перпендикулярны ей. Самая огромная хорда окружности является ее диаметром.

2. Как и любая кривая, окружность имеет некоторую длину p. Давным-давно подмечено, что длина окружности связана с ее диаметром числом ?:p/d=?Отсель следует, что p=?d, либо p = 2?r, где r – радиус окружности .Число ? имеет иррациональное значение, но примерно оно равно 3,14.Зная длину окружности , дозволено и определить площадь кольца, ограниченного двумя окружностями. Она равна:S=2?r*k, где k – расстояние между внутренней и внешней окружностями кольца; 2?r – длина внутренней окружности кольца.

3. Графический метод определения длины окружности , по причине его неточности, применяют редко. Для этого применяют курвиметр – прибор для измерения длины косой линии. В любом месте окружности подмечают исходную точку измерения. К ней подносят курвиметр и ведут его по линии, пока вновь не попадут в ту же точку.

4. Определение длины окружности имеет существенное фактическое значение. Помимо математиков, его доводится осуществлять физикам, астрономам. Первые вычисляют длину окружности элементарных частиц, вторые – небесных тел. Также, зная диаметр цирковой арены, беговой тропинки, руководствуясь приведенными выше формулами, дозволено вычислить, какое расстояние пробежит лошадь либо бегун за один круг.

Совет 5: Как обнаружить угол в равнобедренном треугольнике

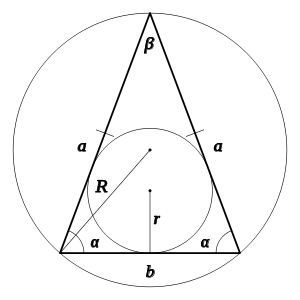
Под равнобедренным треугольником подразумевается такой треугольник, у которого равны между собой 2 стороны, а третья, в свою очередь, именуется основанием равнобедренного треугольника. Для подсчета размеров углов в данном треугольнике существует несколько методов.



Вам понадобится

• Стороны равнобедренного треугольника, один из углов, радиус описанной вокруг треугольника окружности.

Инструкция

1. Возможен, дан равнобедренный треугольник, в котором угол ? – угол при основании равнобедренного треугольника, а ? – противолежащий основанию угол. Тогда, зная один из указанных углов, дозволено рассчитать неведомый:? = (? – ?)/2;? = ? – 2*?. ? – это константа, ее размер принято считать равной 3.14.

2. Если вокруг равнобедренного треугольника с равными сторонами a, основанием b описать окружность радиуса R, то углы ? и ? дозволено будет рассчитать так:? = arcsin(a/2R);? = arcsin(b/2R)

Совет 6: Как обнаружить длину стороны в равнобедренном треугольнике

Равнобедренным именуется треугольник, в котором длины 2-х его сторон идентичны. Дабы вычислить размер какой-нибудь из сторон нужно знать длину иной стороны и один из углов либо радиус описанной вокруг треугольника окружности. В зависимости от знаменитых величин, для расчетов нужно применять формулы, вытекающие из теорем синуса либо косинуса, либо из теоремы о проекциях.

Инструкция

1. Если вестима длина основания равнобедренного треугольника (A) и величина прилежащего к нему угла (угла между основанием и всякий боковой стороной) (α), то вычислить длину всякой из боковых сторон (B) дозволено исходя из теоремы косинусов. Она будет равна частному от деления длины основания на удвоенное значение косинуса знаменитого угла B=A/(2*cos(α)).

2. Длину стороны равнобедренного треугольника, являющейся его основанием (A), дозволено вычислить исходя из той же теоремы косинусов, если знамениты длина его боковой стороны (B) и угол между ней и основанием (α). Она будет равна удвоенному произведению вестимой стороны на косинус вестимого угла A=2*B*cos(α).

3. Иной метод нахождения длины основания равнобедренного треугольника дозволено применять, если вестима величина противолежащего ему угла (β) и длина боковой стороны (B) треугольника. Она будет равна удвоенному произведению длины боковой стороны на синус половины величины знаменитого угла A=2*B*sin(β /2).

4. Подобно дозволено вывести и формулу вычисления боковой стороны равнобедренного треугольника. Если вестима длина основания (A) и величина угла между равными сторонами (β), то длина всей из них (B) будет равна частному от деления длины основания на удвоенный синус половины величины знаменитого угла B=A/(2*sin(β /2)).

5. Если знаменит радиус описанной вокруг равнобедренного треугольника окружности (R), то длины его сторон дозволено рассчитать, зная величину одного из углов. Если знаменита величина угла между боковыми сторонами (β), то длина стороны , являющейся основанием (A), будет равна удвоенному произведению радиуса описанной окружности на синус этого угла A=2*R*sin(β).

6. Если знамениты радиус описанной окружности (R) и величина угла, прилегающего к основанию (α), то длина боковой стороны (B) будет равна удвоенному произведению длины основания на синус вестимого угла B=2*R*sin(α).

Совет 7: Как обнаружить 3-й угол в треугольнике

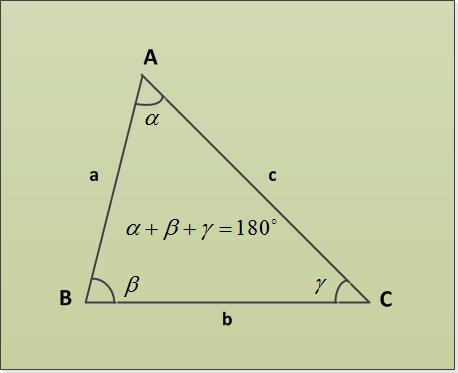
Треугольником называют часть плоскости, ограниченную тремя отрезками прямых (стороны треугольника), имеющих попарно по одному всеобщему концу (вершины треугольника). Углы треугольника дозволено обнаружить по Теореме о сумме углов треугольника.

Инструкция

1. Теорема о сумме углов треугольника гласит, что сумма углов треугольника составляет 180°. Разглядим несколько примеров задач с различными заданными параметрами. Во-первых, пускай заданы два угла ? = 30°, ? = 63°. Нужно обнаружить 3-й угол ?. Находим его непринужденно из теоремы о сумме углов треугольника: ? + ? + ? = 180° => ? = 180° – ? – ? = 180° – 30° – 63° = 87°.

2. Сейчас разглядим задачу нахождения третьего угла треугольника больше всеобщего вида. Пускай нам вестимы три стороны треугольника |AB| = a, |BC| = b, |AC| = c. И нужно обнаружить три угла ?, ? и ?. Воспользуемся теоремой косинусов для нахождения угла ?. Согласно теореме косинусов квадрат стороны треугольника равен сумме квадратов 2-х других сторон минус удвоенное произведение этих сторон и косинуса угла, заключенного между ними. Т.е. в наших обозначениях c^2 = a^2 + b^2 – 2 * a * b * cos ? => cos ? = (a^2 + b^2 – c^2) / (2 *a * b).

3. Дальше воспользуемся теоремой синусов для нахождения угла ?. Согласно этой теореме стороны треугольника пропорциональны синусам противолежащих углов. Выразим из этого соотношения синус угла ?: a/sin ? = b/sin ? => sin ? = b * sin ? / a. 3-й угол находим по теснее знаменитой нам теореме о сумме углов треугольника по формуле ? = 180° – (? + ?).

4. Приведем пример решения сходственной задачи. Пускай даны стороны треугольника a = 4, b = 4 * ?2, c = 4. Из данные мы видим, что это равнобедренный прямоугольный треугольник. Т.е. в итоге мы обязаны получить углы 90°, 45° и 45°. Посчитаем эти углы по приведенному выше методу. По теореме косинусов находим угол ?: cos ? = (16 + 32 – 16) / (2 * 16 * ?2) = 1 / ?2 = ?2 / 2 => ? = 45°. Дальше находим угол ? по теореме синусов: sin ? = 4 * ?2 * ?2 / (2 * 4) = 1 => ? = 90°. И наконец, применив теорему о сумме углов треугольника, получаем угол ? = 180° – 45° – 90° = 45°.

Обратите внимание!
Подметим, что в треугольнике не менее 2-х углов обязаны быть острыми (т.е. поменьше 90°). Следственно посчитав 3-й угол проверьте, удовлетворяют ли углы треугольника заданному условию. Если нет – вы допустили ошибку в вычислениях. В любом случаем будет благотворно сложить все три угла еще раз и удостовериться, что получается 180°.

Полезный совет
Для нахождения величин углов по значениям их тригонометрических функций комфортно пользоваться таблицами Брадиса.

Совет 8: Как обнаружить неведомую сторону в треугольнике

Метод вычисления неведомой стороны треугольника зависит не только от условий задания, но и от того, для чего это делается. С сходственной задачей сталкиваются не только школьники на уроках геометрии, но и инженеры, работающие в различных отраслях производства, дизайнеры интерьера, закройщики и представители многих других профессий. Точность вычислений для различных целей может быть различной, но тезис их остается тем же самым, что и в школьном задачнике.



Вам понадобится

• – треугольник с заданными параметрами;
• – калькулятор;
• – ручка;
• – карандаш;
• – транспортир;
• – лист бумаги;
• – компьютер с программой AutoCAD;
• – теоремы синусов и косинусов.

Инструкция

1. Начертите треугольник, соответствующий условиям задания. Треугольник дозволено возвести по трем сторонам, двум сторонам и углу между ними либо стороне и двум прилегающим к ней углам. Правило работы в тетради и на компьютере в программе AutoCAD в этом плане идентичны. Так что в задании неукоснительно обязаны быть указаны размеры одной либо 2-х сторон и одного либо 2-х углов.

2. При построении по двум сторонам и углу начертите на листе отрезок, равный вестимой стороне. С подмогой транспортира отложите данный угол и проведите вторую сторону , отложив данный в условии размер. Если вам дана одна сторона и два прилежащих к ней угла, начертите вначале сторону , потом от 2-х концов полученного отрезка отложите углы и проведите две другие стороны. Обозначьте треугольник как ABC.

3. В программе AutoCAD комфортнее каждого строить неверный треугольник с подмогой инструмента «Отрезок». Вы обнаружите его через основную вкладку, предпочтя окно «Рисование». Задайте координаты вестимой вам стороны, после этого — финальной точки второго заданного отрезка.

4. Определите вид треугольника. Если он прямоугольный, то незнакомая сторона вычисляется по теореме Пифагора. Гипотенуза равна квадратному корню из суммы квадратов катетов, то есть c=?a2+b2. Соответственно, всякий их катетов будет равно квадратному корню из разности квадратов гипотенузы и знаменитого катета: a=?c2-b2.

5. Для вычисления неведомой стороны треугольника, у которого даны сторона и два прилежащих угла, воспользуйтесь теоремой синусов. Сторона а так относится к sin?, как сторона b к sin?. ? и ? в данном случае — противолежащие углы. Угол, тот, что не задан условиями задачи, дозволено обнаружить, припомнив, что сумма внутренних углов треугольника равна 180°. Вычтите из нее сумму знаменитых вам 2-х углов. Обнаружьте неизвестную вам сторону b, решив пропорцию обыкновенным методом, то есть умножив знаменитую сторону а на sin? и поделив это произведение на sin?. Вы получаете формулу b=a*sin?/sin?.

6. Если вам вестимы стороны a и b и угол ? между ними, используйте теорему косинусов. Незнакомая сторона с будет равна квадратному корню из суммы квадратов 2-х других сторон, минус удвоенное произведение этих же сторон, умноженное на косинус угла между ними. То есть c=?a2+b2-2ab*cos?.

Видео по теме

Совет 9: Как обнаружить длину вписанной окружности

Окружность будет считаться вписанной в многоугольник только в том случае, если все стороны данного многоугольника без исключения касаются данной окружности. Обнаружить длину вписанной окружности дюже легко.

Инструкция

1. Для того дабы узнать длину окружности, необходимо владеть данным о ее радиусе либо диаметре. Радиусом окружности считается отрезок, тот, что соединяет друг с ином центр данной окружности с всякий из точек, принадлежащих окружности. Диаметром окружности является отрезок, тот, что соединяет противоположные друг другу точки окружности, при это непременно проходя через центр окружности. Из определений становится ясно, что радиус окружности в два раза поменьше ее диаметра. Центром окружности является точка, которая в равной степени удалена от всякой из точек на окружности.Формулы, с подмогой которых находится длина окружности, выглядят так:L = ?*D, где D – диаметр окружности;L = 2*?*R, где R – радиус окружности.Пример: Диаметр окружности составляет 20 см, требуется обнаружить ее длину. Решается эта задача с использованием самой первой формулы:L = 3.14*20 = 62.8 смОтвет: Длина окружности диаметром 20 см составляет 62.8 см

2. Определившись с тем, как находится длина окружности, нужно узнать, как обнаружить радиус либо диаметр вписанной в многоугольник окружности. Если в многоугольнике вестима его площадь S, а также его полупериметр P, то обнаружить радиус вписанной окружности дозволено с поддержкой такой формулы:R = S/p

3. Ради понятности представленных выше данных, дозволено разглядеть пример:В четырехугольник вписана окружность. Площадь данного четырехугольника 64 см?, полупериметр его равен 8 см, просится обнаружить длину вписанной в данный многоугольник окружности. Для решения данной задачи нужно исполнить несколько действий. Вначале нужно обнаружить радиус данной окружности:R = 64/8 = 8 смТеперь, зная ее радиус, дозволено, собственно, вычислить и длину данной окружности:L = 2*8*3.14 = 50.24 смОтвет: длина вписанной в многоугольник окружности составляет 50.24 см

Видео по теме

Совет 10: Как вписать треугольник в круг

Если все вершины треугольника лежат на одной окружности, то в этом случае он именуется вписанным, а окружность, соответственно — описанной вокруг него. Возвести треугольник на знаменитой окружности дюже легко, но как вписать треугольник в круг, если первоначально существует именно он?



Вам понадобится

• – циркуль;
• – бумага;
• – карандаш;
• – линейка.

Инструкция

1. Для всякого треугольника неизменно допустимо возвести описанную окружность, от того что эта кривая однозначно определяется тремя заданными точками.Дабы это найти, довольно предположить, что треугольник задан декартовыми координатами своих вершин. В этом случае радиус и координаты центра окружности, проходящей через все три точки, обязаны быть решениями системы из 3 уравнений 2-й степени с тремя незнакомыми.Эта система будет иметь исключительное решение в том случае, если заданные точки не лежат на одной прямой (в этом последнем случае она совсем не имеет решений). Но три точки, лежащие на одной прямой, не могут быть вершинами треугольника, следственно, данный случай дозволено даже не рассматривать. Выходит, решение заведомо существует.

2. Дабы треугольник был вписан в окружность, видимо, требуется, дабы ее центр находился на равном расстоянии от всех 3 его вершин. Задача, таким образом, сводится к нахождению центра описанной окружности.

3. Сторона вписанного треугольника будет являться хордой описанной окружности. Для всякий такой хорды существует перпендикулярный к ней радиус, причем точка их пересечения делит хорду ровно напополам.Следственно, всякий срединный перпендикуляр треугольника (то есть прямая, проходящая через середину его стороны и перпендикулярная ей) проходит через центр описанной окружности. Довольно провести два таких перпендикуляра, и точка их пересечения будет центром. Радиус же описанной окружности однозначно определяется расстоянием до всякий из вершин.

4. Процедура деления отрезка напополам циркулем и линейкой представляет собой, по сути, построение срединного перпендикуляра. Таким образом, задача нахождения центра описанной окружности сводится к делению циркулем и линейкой 2-х сторон треугольника.

5. Если данный треугольник — прямоугольный, то центр описанной окружности совпадает с серединой его гипотенузы.

Видео по теме

Совет 11: Как обнаружить центр вписанной окружности

Окружность может быть вписана в угол либо в рельефный многоугольник. В первом случае она касается обеих сторон угла, во втором — всех сторон многоугольника. Расположение ее центра в обоих случаях вычисляется схожими методами. Нужно провести добавочные геометрические построения.



Вам понадобится

• – многоугольник;
• – угол заданного размера;
• – окружность с заданным радиусом;
• – циркуль;
• – линейка;
• – карандаш;
• – калькулятор.

Инструкция

1. Обнаружить центр вписанной окружности обозначает определить его расположение касательно вершины отдельно взятого угла либо углов многоугольника. Припомните, где находится центр окружности , вписанной в угол. Он лежит на биссектрисе. Постройте угол заданного размера и поделите его напополам. Радиус вписанной окружности вы знаете. У вписанной окружности он же является и кратчайшим расстоянием от центра до касательной, то есть перпендикуляром. Касательной в данном случае является сторона угла. Постройте к одной из сторон перпендикуляр, равный заданному радиусу. Финальная его точка должна находиться на биссектрисе. У вас получился прямоугольный треугольник. Назовите его, скажем, ОСА. О — это вершина треугольника и единовременно центр окружности , ОС — радиус, а ОА — отрезок биссектрисы. Угол ОАС равен половине начального угла. По теореме синусов обнаружьте отрезок ОА, тот, что является гипотенузой.

2. Для определения местоположения центра вписанной окружности в многоугольнике исполните схожие построения. Стороны всякого многоугольника по определению являются касательными к вписанной окружности . Соответственно, радиус, проведенный к всякий точке касания, будет ей перпендикулярен. В треугольнике центр вписанной окружности является точкой пересечения биссектрис, то есть расстояние его от углов определяется верно так же, как и в предыдущем случае.

3. Окружность, вписанная в многоугольник, единовременно является вписанной и в весь его угол. Это следует из ее определения. Соответственно, расстояние центра от всякой из вершин дозволено вычислить верно так же, как и в случае с отдельно взятым углом. Это исключительно главно помнить, если вы имеете дело с неправильным многоугольником. При вычислениях ромба либо квадрата довольно провести диагонали. Центр совпадет с точкой их пересечения. Определить его расстояние от вершин квадрата дозволено по теореме Пифагора. В случае с ромбом действует теорема синусов либо косинусов, в зависимости от того, какой угол вы используете для вычислений.

Совет 12: Как обнаружить длину вписанной окружности в треугольник

Если все точки внутри периметра круга не выходят за пределы периметра треугольника и при этом периметр круга имеет каждого по одной всеобщей точке с всякой из сторон треугольника, то окружность именуется вписанной в треугольник. Существует каждого одно значение радиуса круга, при котором его дозволено вписать в треугольник с заданными параметрами. Это качество вписанного круга дозволяет по параметрам треугольника вычислить и его параметры, включая длину окружности.

Инструкция

1. Начните вычисление длины вписанной в треугольник окружности (l) с определения ее радиуса (r). Если знаменита площадь многоугольника (S) и длины всех его сторон (a, b и c), то радиус будет равен отношению удвоенной площади к сумме этих длин r=2*S/(a+b+c).

2. Используйте геометрическое определение константы Пи для вычисления длины окружности по вестимому значению радиуса. Эта константа выражает отношение длины окружности к ее диаметру, то есть удвоенному радиусу. Значит, для нахождения длины окружности вам следует умножить полученное на предыдущем шаге значение радиуса на удвоенное число Пи. В всеобщем виде эту формулу дозволено записать так: l=4*?*S/(a+b+c).

3. Если площадь треугольника незнакома, но дана величина одного из его углов (?) и длины всех сторон (a, b и c), то радиус вписанной окружности (r) дозволено выразить через тангенс угла ?. Для этого вначале сложите длины всех сторон и поделите итог напополам, потом отнимите от полученного значения длину той стороны (a), которая лежит наоборот угла знаменитой величины. Полученное число нужно умножить на тангенс половины знаменитой величины угла: r=((a+b+c)/2-a)*tg(?/2). Если этой формулой во втором шаге заменить выражение из первого шага, то формула длины окружности примет такой вид: l=2*?*((a+b+c)/2-a)*tg(?/2).

4. Дозволено обойтись и только длинами сторон треугольника (a, b и c). Но в этом случае для облегчения формулы отличнее ввести дополнительную переменную – полупериметр треугольника: p=(a+b+c)/2. С ее подмогой радиус вписанной окружности дозволено выразить как квадратный корень из частного от деления произведения разности полупериметра и длины всякой из сторон на полупериметр: r=?((p-a)*(p-b)*(p-c)/p). А формула длины вписанной окружности в этом случае приобретет такой вид: l=2*?*?((p-a)*(p-b)*(p-c)/p).

Видео по теме

Совет 13: Как обнаружить длину высоты в равнобедренном треугольнике

Высотами в треугольнике называют три отрезка прямых, весь из которых перпендикулярен одной из сторон и соединяет ее с противолежащей вершиной. Как минимум две стороны и два угла в равнобедренном треугольнике имеют идентичные величины, следственно и длины 2-х высот обязаны быть равны. Это обстоятельство гораздо упрощает вычисление длин высот фигуры.

Инструкция

1. Высоту (Hc), проведенную к основанию равнобедренного треугольника, дозволено рассчитать, зная длины этого основания (c) и боковой стороны (a). Для этого дозволено применять теорему Пифагора, потому что высота, боковая сторона и половина основания образуют прямоугольный треугольник. Высота и половина основания в нем являются катетами, следственно для решения задачи извлеките корень из разности между возведенной в квадрат длиной боковой стороны и четвертью квадрата длины основания: Hс = ?(a?-?*c?).

2. Эту же высоту (Hc) дозволено вычислить и по длине всякий из сторон, если в условиях приведена величина правда бы одного угла. Если это угол при основании треугольника (?) а знаменитая длина определяет величину боковой стороны (a), для приобретения итоге перемножьте длину знаменитой стороны и синус вестимого угла: Hс = a*sin(?). Эта формула вытекает из теоремы синусов.

3. Если вестима длина основания (с) и величина прилегающего к нему угла (?), для вычисления высоты (Hc), половину длины основания умножьте на синус вестимого угла и поделите на синус разницы между 90° и величиной того же угла: Hс = ?*c*sin(?)/sin(90°-?).

4. При знаменитых размерах основания (с) и противолежащего ему угла (?) для вычисления высоты (Hc) умножайте половину длины вестимой стороны на синус разницы между 90° и половиной вестимого угла, а итог разделяете на синус половины того же угла: Hс = ?*c*sin(90°-?/2)/sin(?/2). Эта формула, как и две предыдущие, вытекает из теоремы синусов в сочетании с теоремой о сумме углов в треугольнике .

5. Длину высоты, проведенной к одной из боковых сторон (Ha) дозволено вычислить, скажем, зная длину этой стороны (a) и площадь равнобедренного треугольника (S). Дабы это сделать, обнаружьте удвоенную величину соотношения между площадью и длиной знаменитой стороны: Ha = 2*S/a.

Совет 14: Как вычислять длину окружности и площадь круга

Окружностью называют рубеж круга – замкнутую кривую линию, длина которой зависит от размера круга . Эта замкнутая линия делит безграничную по определению плоскость на две неравные части, одна из которых продолжает оставаться безмерной, а иная может быть измерена и именуется площадью круга . Обе величины – длина окружности и площадь круга – определяются его размерами и могут быть выражены одна через иную либо через диаметр этой фигуры.

Инструкция

1. Для расчета длины окружности (L) с применением знаменитой длины диаметра (D) не обойтись без числа Пи – математической константы, которая, собственно, и выражает взаимозависимость этих 2-х параметров круга . Перемножьте число Пи и диаметр, дабы получить желанную величину L = ?*D. Зачастую взамен диаметра в начальных данные приводится радиус (R) круга . В этом случае замените в формуле диаметр удвоенным радиусом: L = ?*2*R. Скажем, при радиусе в 38 см длина окружности должна составить приблизительно 3,14*2*38 = 238,64 см.

2. Рассчитать площадь круга (S) при знаменитом диаметре (D) тоже нереально без применения числа Пи – умножайте его на возведенный в квадрат диаметр, а итог разделяете на четверку: S = ?*D?/4. С применением радиуса (R) эта формула станет на одно математическое действие короче: S = ?*R?. Скажем, если радиус равен 72 см, площадь должна составить 3,14*722 = 16277,76 см?.

3. Если необходимо выразить длину окружности (L) через площадь круга (S), сделайте это с применением приведенных в 2-х предыдущих шагах формул. В них есть один всеобщий параметр круга – диаметр, либо удвоенный радиус. Вначале выразите неведомый радиус через вестимую площадь круга , дабы получить такое выражение: ?(S/?). После этого подставьте это значение в формулу из первого шага. Окончательная формула расчета длины окружности по вестимой площади круга должна выглядеть так: L = 2*?(?*S). Скажем, если круг занимает площадь в 200 см?, длина его окружности будет равна 2*?(3,14*200) = 2*?628 ? 50,12 см.

4. Обратная задача – нахождение площади круга (S) по знаменитой длине окружности (L) – затребует от вас схожей последовательности действий. Вначале выразите из формулы первого шага радиус через длину окружности – у вас должно получиться такое выражение: L/(2*?). После этого подставьте его в формулу второго шага – итог должен выглядеть так: S = ?*(L/(2*?))? = L?/(4*?). Скажем, площадь круга с длиной окружности в 150 см должна составлять примерно 1502/(4*3,14) = 22500/12,56 ? 1791,40 см?.

Видео по теме

Совет 15: Как обнаружить угол между касательными

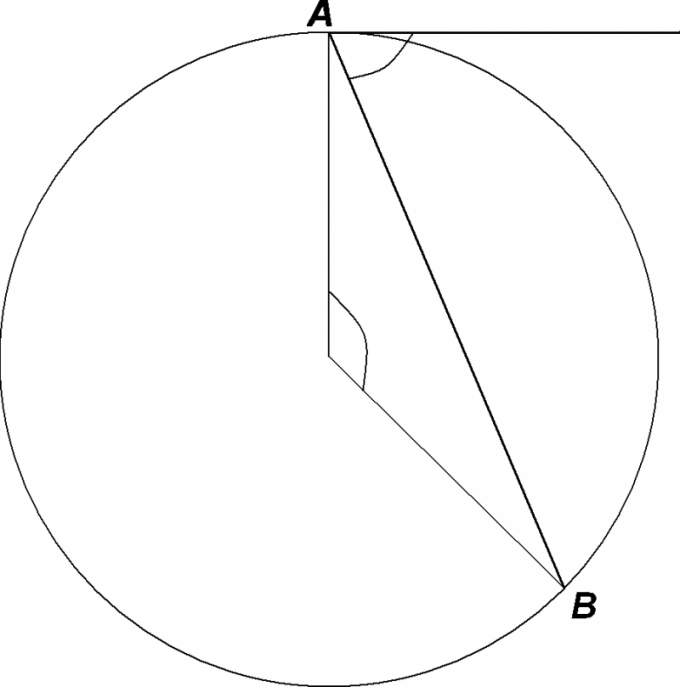
Прямая линия, имеющая с окружностью одну всеобщую точку, является касательной к окружности. Иная специфика касательной – она неизменно перпендикулярна радиусу, проведенному в точку касания, то есть касательная и радиус образуют прямой угол . Если из одной точки А проведены две касательных к окружности АВ и АС, то они неизменно равны между собой. Определение угла между касательными (угол АВС) производится с поддержкой теоремы Пифагора.

Инструкция

1. Для определения угла нужно знать радиус окружности ОВ и ОС и расстояние точки начала касательной от центра окружности – О. Выходит, углы АВО и АСО равны 90 градусов, радиус ОВ, скажем 10 см, а расстояние до центра окружности АО равно 15 см. Определите длину касательной по формуле в соответствии с теоремой Пифагора: АВ = квадратный корень из АО2 – ОВ2 либо 152 – 102 = 225 – 100 = 125;



2. Извлеките квадратный корень. Получится 11.18 см. От того что угол ВАО представляет собой sin либо отношение сторон ВО и АО вычислите его значение: Sin угла ВАО = 10 : 15 = 0.66

3. После этого, пользуясь таблицей синусов, обнаружьте данное значение, которое соответствует приблизительно 42 градусам. Таблица синусов применяется для решения разных задач – физических, математических либо инженерных. Остается узнать величину угла ВАС, для чего следует величину данного угла удвоить, то есть, получится приблизительно 84 градусов.

4. Величина центрального угла соответствует угловой величине дуги, на которую он опирается. Величину угла дозволено также определить с подмогой транспортира, приложив его к чертежу. Потому что сходственные вычисления относятся к тригонометрии, то дозволено воспользоваться тригонометрическим кругом. С его поддержкой дозволено переводить градусы в радианы и напротив.

5. Как знаменито, полный круг составляет 360 градусов либо 2П радиан. На тригонометрическом круге отображены значения синусов и косинусов основных углов. Стоит напомнить, что значение синуса находится на оси Y, а косинуса на оси Х. Значения синуса и косинуса находятся в интервале от -1 до 1.

6. Определить значения тангенса и котангенса угла дозволено поделив синус на косинус, а котангенса напротив – косинуса на синус. Тригонометрический круг дозволяет определить знаки всех тригонометрических функций. Так, синус – это нечетная функция, а косинус – четная. Тригонометрический круг разрешает осознать, что синус и косинус – периодические функции. Как знаменито, период равен 2П.

Видео по теме