Совет 1: Как обнаружить площадь сечения шара

Пускай дан шар с радиусом R, тот, что на некотором расстоянии b от центра пересекает плоскость. Расстояние b поменьше либо равно радиусу шара . Требуется обнаружить площадь S получающегося при этом сечения.

Инструкция

1. Видимо, что если расстояние от центра шара до плоскости равно радиусу плоскости, то плоскость касается шара только в одной точке, и площадь сечения будет равна нулю, то есть если b = R, то S = 0. Если b = 0, то секущая плоскость проходит через центр шара. В этом случае сечение будет представлять собой круг, радиус которого совпадает с радиусом шара. Площадь этого круга будет, согласно формуле, равна S = ?R^2.

2. Эти два крайних случая дают границы, между которыми неизменно будет лежать желанная площадь: 0 < S < ?R^2. При этом всякое сечение шара плоскостью неизменно является кругом. Следственно, задача сводится к тому, дабы обнаружить радиус окружности сечения. Тогда площадь этого сечения вычисляется по формуле площади круга.

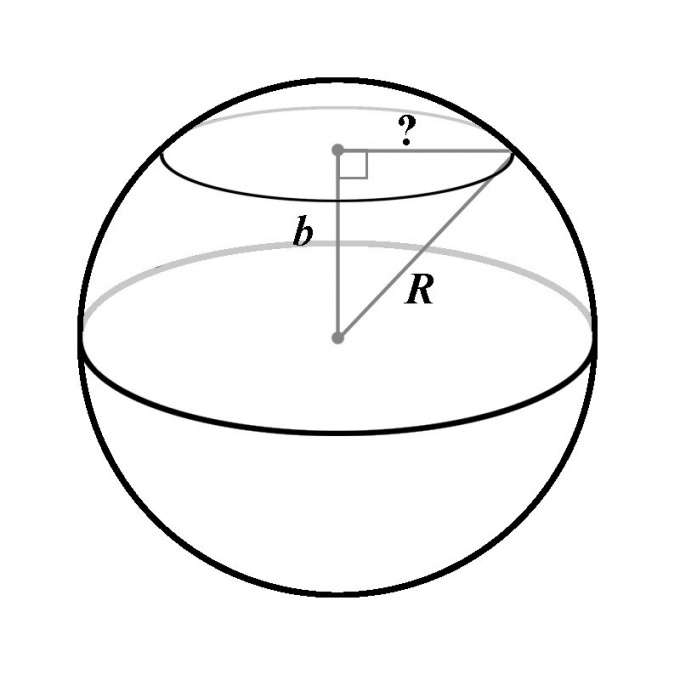
3. От того что расстояние от точки до плоскости определяется как длина отрезка, перпендикулярного плоскости и начинающегося в точке, 2-й конец этого отрезка будет совпадать с центром окружности сечения. Такой итог вытекает из определения шара: видимо, что все точки окружности сечения принадлежат сфере, а следственно, лежат на равном расстоянии от центра шара. Это значит, что всякая точка окружности сечения может считаться вершиной прямоугольного треугольника, гипотенузой которого служит радиус шара, одним из катетов — перпендикулярный отрезок, соединяющий центр шара с плоскостью, а вторым катетом — радиус окружности сечения.

4. Из 3 сторон этого треугольника заданы два — радиус шара R и расстояние b, то есть гипотенуза и катет. По теореме Пифагора длина второго катета должна быть равна ?(R^2 – b^2). Это и есть радиус окружности сечения. Подставляя обнаруженное значение радиуса в формулу площади круга, легко прийти к итогу, что площадь сечения шара плоскостью равна:S = ?(R^2 – b^2).В частных случаях, когда b = R либо b = 0, выведенная формула всецело согласуется с теснее обнаруженными итогами.

Совет 2: Как обнаружить площадь шара

Все планеты ясной системы имеют форму шара . Помимо того, шарообразную либо близкую к таковой форму имеют и многие объекты, сделанные человеком, включая детали технических устройств. Шар, как и всякое тело вращения, имеет ось, которая совпадает с диаметром. Впрочем это не исключительное главное качество шара . Ниже рассмотрены основные свойства этой геометрической фигуры и метод нахождения ее площади.

Инструкция

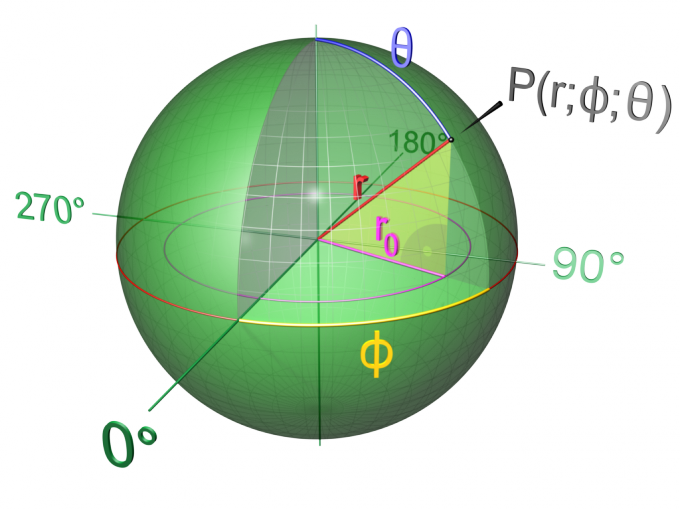
1. Если взять полукруг либо круг и провернуть его вокруг своей оси, получится тело, называемое шаром. Иными словами, шаром именуется тело, ограниченное сферой. Сфера представляет собой оболочку шара , и ее сечением является окружность. От шара она отличается тем, что является полой. Ось как у шара , так и у сферы совпадает с диаметром и проходит через центр. Радиусом шара именуется отрезок, проложенный от его центра до всякий внешней точки. В противоположность сфере, сечения шара представляют собой круги. Форму, близкую к шарообразной, имеет множество планет и небесных тел. В различных точках шара имеются идентичные по форме, но неодинаковые по величине, так называемые сечения – круги различной площади.

2. Шар и сфера – взаимозаменяемые тела, в различие от конуса, невзирая на то, что конус также является телом вращения. Сферические поверхности неизменно в своем сечении образуют окружность, само­стоятельно от того, как именно она вращается – по горизонтали либо по вертикали. Коническая же поверхность получается лишь при вращении треугольника по его оси, перпендикулярной основанию. Следственно конус, в различие от шара , и не считается взаимозаменяемым телом вращения.

3. Самый крупный из допустимых кругов получается при сечении шара плоскостью, проходящей через центр О. Все круги, которые проходят через центр О, пересекаются между собой в одном диаметре. Радиус неизменно равен половине диаметра. Через две точки A и B, располагающиеся в любом месте поверхности шара , может проходить безмерное число кругов либо окружностей. Именно по этой причине через полюса Земли может быть проведено неограниченное число меридианов.

4. При нахождении площади шара рассматривается, раньше каждого, площадь сферической поверхности.Площадь шара , а вернее, сферы, образующей его поверхность, может быть рассчитана на основании площади круга с тем же радиусом R. От того что площадь круга есть произведение полуокружности на радиус, его дозволено рассчитать дальнейшим образом:S = ?R^2Так как через центр шара проходят четыре основных крупных круга, то, соответственно площадь шара (сферы) равна:S = 4 ?R^2

5. Данная формула может быть пригодна в том случае, если вестим либо диаметр, либо радиус шара либо сферы. Впрочем, эти параметры приведены в качестве условий не во всех геометрических задачах. Существуют и такие задачи, в которых шар вписан в цилиндр. В этом случае, следует воспользоваться теоремой Архимеда, суть которой заключается в том, что площадь поверхности шара в полтора раза поменьше полной поверхности цилиндра:S = 2/3 S цил., где S цил. –площадь полной поверхности цилиндра.

Видео по теме


Видео по теме