Совет 1: Как обнаружить периметр многоугольника

Всякий день мы встречаемся с многоугольниками. Даже план квартиры либо садового участка состоит из многоугольников. Для того дабы рассчитать нужное число досок на возведение забора либо сколько рулонов обоев надобно на оклейку стен в квартире, неизменно вначале измеряют периметр многоугольной фигуры. Периметром многоугольника называют сумму длин его сторон. В зависимости от типа многоугольника и приборов для измерения длины методы нахождения периметра фигуры могут быть разными.



Вам понадобится

• – линейка
• – нитка
• – ножницы

Инструкция

1. Если измеряемый многоугольник верный, то есть у него все стороны и углы равны, то для нахождения периметра измерьте длину одной из его сторон с подмогой линейки. После этого посчитайте число углов многоугольника, которое равно число его сторон. Получившееся число умножьте на длину стороны фигуры. Это будет периметр многоугольника.

2. Если многоугольник симметричный и имеет 2 либо 4 пары равного комплекта сторон, то измерьте вначале длину сторон на одном из повторяющихся участков. После этого сложите полученные значения и для приобретения периметра фигуры умножьте эту сумму на число повторяющихся частей в многоугольнике.

3. Дабы обнаружить периметр квадрата, то измерьте одну из сторон и умножьте полученное значение на четыре. Если перед вами пятиугольник, то на четыре; если шестиугольник, то на шесть.

4. Для вычисления периметра многоугольника, у которого все стороны имеют различную длину, измерьте линейкой всякую из сторон. После этого, сложив полученные числа, вы получите периметр многоугольника.

5. Если вы не хотите всякий раз при измерении сторон соотносить точку отсчета длины на линейке либо рулетке с углом многоугольника, то проложите по кромке фигуры обыкновенную веревку. В том месте, где средство измерения, обойдя стороны фигуры, коснется своего кончика, отрежьте ее ножницами. Длина измерительной нити будет равна периметру многоугольной фигуры. Для нахождения численного значения периметра примитивно измерьте длину веревки с подмогой линейки либо рулетки.

6. При нахождении периметра трудного многоугольника, тот, что дозволено разбить на несколько различных многоугольников, вначале обнаружьте длины сторон всякой из фигур, которые образуют непростой силуэт, а после этого сложите получившиеся числа. Такой метод классен, если трудная фигура состоит из положительных многоугольников, подсчитать периметр которых легче, чем фигур с различными длинами сторон.

Совет 2: Как находить периметр квадрата

Квадрат – прекрасная и простая плоская геометрическая фигура. Это прямоугольник с равными сторонами. Как же обнаружить периметр квадрата , если знаменита длина его стороны?

Инструкция

1. Раньше каждого, стоит припомнить, что периметр есть ни что иное как сумма длин сторон геометрической фигуры. Рассматриваемый нами квадрат имеет четыре стороны. Больше того, по определению квадрата , все эти стороны равны между собой.Из этих предпосылок вытекает простая формула для нахождения периметр а квадрата – периметр квадрата равен длине стороны квадрата , умноженной на четыре:Р = 4а, где а – длина стороны квадрата .

Видео по теме

Совет 3: Как обнаружить периметр фигуры

В задачах по геометрии зачастую требуется обнаружить периметр фигуры . Периметром фигуры именуется длина ограничивающей ее линии. Дозволено, безусловно, примитивно измерить длину этой линии. Впрочем, итоги таких измерений могут оказаться неудовлетворительно точными. Помимо того, измерение длины косой линии – достаточно-таки сложный процесс. Следственно на практике и при решении геометрических задач обыкновенно применяют особые формулы.



Вам понадобится

• линейка, циркуль, калькулятор

Инструкция

1. Дабы обнаружить периметр фигуры , ограниченной ломаной линией, сложите длины всех составляющих ее отрезков. Если длины отрезков незнакомы, измерьте их с подмогой циркуля и линейки. Если фигура имеет относительно крупные размеры, воспользуйтесь рулеткой. Единицей измерения периметр а будут служить те же единицы, в которых заданы (измерялись) длины составляющих отрезков. Если единицы измерения различные, то их нужно привести к одному виду.Скажем, если земельный участок имеет треугольную форму с длинами сторон 10, 20 и 30 метров, соответственно, то его периметр составит: 10 + 20 + 30 (м).

2. Для нахождения периметр а примитивных геометрических фигур, воспользуйтесь особыми формулами.Дабы обнаружить периметр ромба (в частности, квадрата), умножьте длину его стороны на четыре. То есть, воспользуйтесь следующими формулами:П(ромб) = П(квадрат) = 4 * с,где с – длина стороны ромба (квадрата), П – его периметр .

3. Для нахождения периметр а параллелограмма (в частности, прямоугольника), сложите его длину и ширину и умножьте на два (под длиной и шириной подразумеваются длины 2-х смежных сторон). Нагляднее, это дозволено записать в дальнейшем виде:П(параллелограмм) = П(прямоугольник) = 2 * (д + ш), где:д и ш – длина и ширина параллелограмма (прямоугольника), соответственно.

4. Дабы обнаружить периметр круга, вычислите длину ограничивающей его окружности. Для этого воспользуйтесь классической формулой:П(круг) = ? * Д илиП(круг) = 2 * ? * Р,где: Д – диаметр круга, Р – радиус круга, ? – число «пи», приблизительно равное 3,14.

5. Если вестима длина диагонали квадрата, то для нахождения его периметр а используйте следующую формулу:П(квадрат) = 2?2 * д,где д – длина диагонали квадрата.

6. Периметр квадрата дозволено рассчитать, применяя информацию о его площади. Для этого воспользуйтесь дальнейшим правилом:П(квадрат) = 4 * ?Sкв,где Sкв – площадь квадрата.

Совет 4: Как обнаружить периметр пятиугольника

Нахождение периметра пятиугольника – задача, требующая обширных теоретических умений, пространственного и логичного мышления. Значимо также и верно оформить решение.



Вам понадобится

• – Тетрадь;
• – линейка;
• – карандаш;
• – ручка;
• – калькулятор.

Инструкция

1. Пятиугольник – это многоугольник с пятью углами. Пятиугольники бывают верными и неправильными. Положительный пятиугольник — это рельефный многоугольник, у которого все стороны и все углы равны между собой.Неверный пятиугольник – это многоугольник, стороны и углы которого не равны. В базовом курсе геометрии почаще рассматриваются верные пятиугольники.

2. Периметр многоугольника – это сумма длин всех его сторон. Дабы обнаружить периметр пятиугольника, вычислите длину всей стороны, а после этого сложите их.

3. Если в задаче дано, что сторона верного пятиугольника АВСDF равна 5 см, то периметр его будет равен:P = 5АВP = 5*5 = 25В данном случае вы примитивно умножаете длину стороны пятиугольника на число сторон, т.к. все они равны между собой (Рис.1).

4. Если же в задании вам встретился неверный пятиугольник, то вы обязаны вначале обнаружить длину всей его стороны, а потом сложить их.

5. К примеру, в задаче говорится, что ВО = 8, ОF = 4, ВС = 7, угол ВОА = 90, угол ОАМ = 45, ОМ = 3, АВ = DF, ВС = СD. Сначала разглядите треугольник АОВ: ВО = 8. Из данные следует, что АО = ОF = 4. Треугольник АОВ является прямоугольным. АО и ОF – катеты, АВ – гипотенуза. По теореме Пифагора, квадрат гипотенузы равен сумме квадратов катетов.

6. Следственно, АВ ^2 = АО ^2 + ОF ^2.АВ ^2 = 8^2 + 4^2АВ ^2 = 64 + 16АВ ^2 = 80АВ = ?80АВ = 8,94АВ = DF = 8,94.

7. После этого разглядите треугольник АОF. АО = ОF = 4, ОМ = 3. Угол АОВ = DОF = 90 (как накрест лежащие). Следственно, АОМ = ВОD (как накрест лежащие), и значит АОМ + ВОD = 360 – АОВ + DОF = 180. АОМ = 90.Отсель следует, что треугольник АОF – прямоугольный.Значит угол АМО = АОМ – ОАМ,АМО = 90 – 45, АМО = 45.

8. Следственно, треугольник АОF – равнобедренный. А в равнобедренных треугольниках наоборот равных углов лежат равные стороны. Значит АМ = ОМ = 3.Отсель АF = 2АМ = 6.

9. Сейчас вы можете вычислить периметр пятиугольника АВСDF.Р = 8,94*2+7*2+6Р = 37,88

Совет 5: Как обнаружить число сторон многоугольника

Многоугольник состоит из нескольких отрезков, объединенных между собой и образующих замкнутую линию. Все фигуры этого класса делятся на примитивные и трудные. К простым относятся треугольник и четырехугольник, а к трудным – многоугольники с огромным числом сторон , а также звездчатые многоугольники.

Инструкция

1. Особенно зачастую в задачах встречается правильный треугольник со сторон ой a. От того что многоугольник является верным, то все три его сторон ы равны. Следственно, зная медиану и высоту треугольника, дозволено обнаружить все его сторон ы. Для этого используйте метод нахождения сторон ы через синус:a=x/cos?.Потому что сторон ы треугольника равны, т.е. a=b=c=a, a=b=c=x/cos?, где x – высота, медиана либо биссектриса.Аналогичным образом находите все три неведомые сторон ы в равнобедренном треугольнике, но при одном условии – заданной высоте. Она должна проецироваться на основание треугольника. Зная высоту основания x, обнаружьте сторон у равнобедренного треугольника a:a=x/cos?.От того что a=b, потому что треугольник равнобедренный, обнаружьте его сторон ы дальнейшим образом:a=b=x/cos?.Позже того как вы обнаружили боковые сторон ы треугольника, вычислите длину основания треугольника, применяя теорему Пифагора для нахождения половины основания:c/2=?(x/cos?)^2-(x^2)=?x^2 (1-cos^2?)/ cos^2?=xtg?.Отсюда найдите основание:c=2xtg?.

2. Квадрат представляет собой верный четырехугольник, сторон ы которого вычисляются несколькими методами. Ниже рассмотрен всякий из них.1-й метод предлагает нахождение сторон ы через диагональ квадрата. От того что все углы у квадрата прямые, данная диагональ делит их напополам таким образом, что образуются два прямоугольных треугольника с углами 45 градусов при основании. Соответственно, сторон а квадрата равна:a=b=c=f=d*cos?=d?2/2, где d – диагональ квадрата.Если квадрат вписан в окружность, то зная радиус этой окружности, обнаружьте его сторон у:a4=R?2, где R – радиус окружности.

3. У многосторон них многоугольников сторон у вычисляйте последним из предложенных методов – путем вписывания многоугольника в окружность. Для этого начертите положительный многоугольник с произвольными сторон ами, а вокруг него опишите окружность с заданным радиусом R.Представьте себе, что в задаче дан определенный произвольный n-угольник. Если окружность описана около этого многоугольника , то для нахождения сторон ы примените формулу:an=2Rsin?/2.

Видео по теме

Совет 6: Как обнаружить периметр верного многоугольника

Периметром многоугольника называют замкнутую ломаную линию, составленную из всех его сторон. Нахождение длины этого параметра сводится к суммированию длин сторон. Если все отрезки, образующие периметр такой двухмерной геометрической фигуры, имеют идентичные размеры, многоугольник именуется верным. В этом случае вычисление периметра гораздо упрощается.

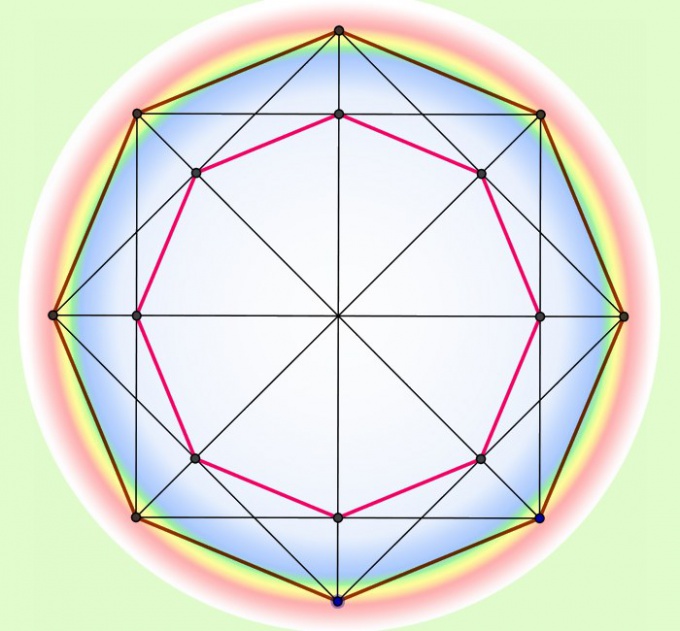
Инструкция

1. В самом простом случае, когда знамениты длина стороны (а) положительного многоугольника и число вершин (n) в нем, для вычисления длины периметра (Р) легко перемножьте эти две величины: Р = а*n. Скажем, длина периметра верного шестиугольника со стороной в 15 см должна быть равна 15*6=90 см.

2. Вычислить периметр такого многоугольника по вестимому радиусу (R) описанной около него окружности тоже допустимо. Для этого придется вначале выразить длину стороны с применением радиуса и числа вершин (n), а после этого умножить полученную величину на число сторон. Дабы рассчитать длину стороны умножьте радиус на синус числа Пи, поделенного на число вершин, а итог удвойте: R*sin(?/n)*2. Если вам комфортнее вычислять тригонометрическую функцию в градусах, замените число Пи на 180°: R*sin(180°/n)*2. Периметр вычислите умножением полученной величины на число вершин: Р = R*sin(?/n)*2*n = R*sin(180°/n)*2*n. Скажем, если шестиугольник вписан в круг с радиусом 50 см, его периметр будет иметь длину 50*sin(180°/6)*2*6 = 50*0,5*12 = 300 см.

3. Схожим методом дозволено посчитать периметр, не зная длины стороны положительного многоугольника , если он описан около окружности с знаменитым радиусом (r). В этом случае формула для вычисления размера стороны фигуры будет отличаться от предыдущей лишь задействованной тригонометрической функцией. Замените в формуле синус на тангенс, дабы получить такое выражение: r*tg(?/n)*2. Либо для расчетов в градусах: r*tg(180°/n)*2. Для вычисления периметра увеличьте полученную величину в число раз, равное числу вершин многоугольника : Р = r*tg(?/n)*2*n = r*tg(180°/n)*2*n. Скажем, периметр восьмиугольника, описанного вблизи круга с радиусом в 40 см, будет примерно равен 40*tg(180°/8)*2*8 ? 40*0,414*16 = 264,96 см.

Совет 7: Периметр многоугольника: как рассчитать правильно

Линия, ограничивающая занимаемую плоской геометрической фигурой площадь, именуется периметром . В многоугольнике эта ломаная линия включает в себя все стороны, следственно для вычисления длины периметра нужно знать длину всей из сторон. В верных многоугольниках длины отрезков между вершинами идентичны, что дозволяет упростить расчеты.

Инструкция

1. Для вычисления длины периметра неправильного многоугольника вам придется выяснять доступными средствами длину всякой из сторон по отдельности. Если эта фигура изображена на чертеже, определите размеры сторон, скажем, с поддержкой линейки и сложите полученные величины – итог и будет желанным периметром .

2. Многоугольник может быть задан в условиях задачи координатами своих вершин. В этом случае ступенчато рассчитайте длину всякой из сторон. Используйте координаты точек (скажем A(X?,Y?), B(X?,Y?)), ограничивающих отрезки, которые являются сторонами фигуры. Обнаружьте разность координат этих 2-х точек по всей из осей (X?-X? и Y?-Y?), возведите полученные величины в квадрат и сложите. После этого извлеките корень из полученного значения: ?((X?-X?)? + (Y?-Y?)?) – это и будет длина стороны между вершинами A и B. Проделайте эту операцию для всей пары соседних вершин, позже чего сложите рассчитанные длины сторон, дабы узнать длину периметра.

3. Если в условиях задачи сказано, что многоугольник является верным, а также дано число его вершин либо сторон, для нахождения периметра довольно вычисления длины лишь одной стороны. Если знамениты координаты, рассчитайте ее описанным выше методом, а полученное значение увеличьте в число раз, равное числу сторон, дабы вычислить периметр.

4. При знаменитом из условий задачи числе сторон (n) положительного многоугольника и диаметре (D) описанной около него окружности, длину периметра (P) дозволено вычислить с применением тригонометрической функции – синуса. Длину стороны определите умножением вестимого диаметра на синус угла, величина которого равна 180°, поделенным на число сторон: D*sin(180°/n). Для вычисления периметра, как было сказано в предыдущем шаге, умножьте полученное значение на число сторон: P = D*sin(180°/n)*n.

5. По вестимому диаметру (d) окружности, вписанной в положительный многоугольник с заданным числом вершин (n), тоже дозволено определить периметр (Р). В этом случае формула расчета будет отличаться от описанной в предыдущем шаге только примененной в ней тригонометрической функцией – замените синус на тангенс: P = d*tg(180°/n)*n.

Видео по теме

Совет 8: Что такое многоугольник конкурентоспособности

Конкурентоспособность является представлением, характеризующим вероятности объекта либо субъекта производства обогнать аналогов в имеющихся обстоятельствах. Данные о данном показателе помогают возвести истинную картину касательно востребованности продукта.


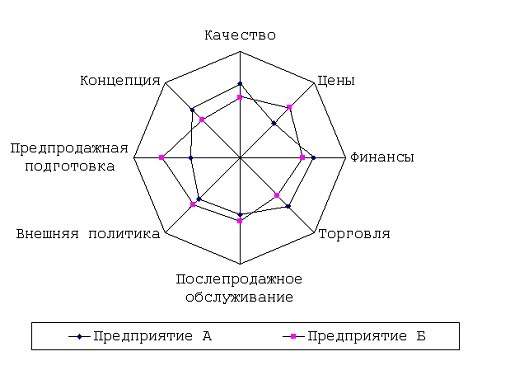
Такая информация содействует возникновению направляющих последующего становления бизнеса и образованию готовности к переменам. Последнее весьма главно для стремительной приспосабливаемости к новым условиям. Инвесторы, покупатели, изготовители, государство используют многообразные способы оценки конкурентоспособности. Безусловно, что всякий из субъектов осуществляет обзор, базируясь на приобретении выгоды в условиях современного рынка. К примеру, инвестор для выбора объекта вложений анализирует степень притягательности региона либо определенного предприятия. Учитывается и рациональность теснее сделанных инвестиций. Способы обнаружения степени конкурентоспособности обязаны брать в расчет добротные колляции продукции, ценовое соотношение с аналогами, ярус сервиса клиентов, производительность применяемых рекламных спецтехнологий.

Что включает в себя многоугольник конкурентоспособности

Сходственный способ сравнительной оценки довольно внятен для воспринятия и помогает сопоставлять товары, службы и предприятия между собой. Для этого на чертеже отображаются расположения сопоставляемых объектов по каждому показателям. Многоугольник формируется на основе бесчисленных колляций, которые представлены на рисунке векторами, выходящими из одной точки в различные стороны. Среди них дозволено выделить следующие:- Цена службы либо продукта;- Главная доктрина товара/услуги;- Уровень квалификации персонала при продаже;- Сервисное обслуживание (доставка, сборка, ручательство и ремонт);- Объем рынка сбыта продукции (именные магазины, салоны);- Финансовое благополучие предприятия;- Опытность фирмы либо новинка продукта;- Степень информационного могущества на покупателя (присутствие собственного сайта, концептуальная реклама).Безусловно, что вышеозвученные моменты являются лишь приблизительными значениями для осей, от того что всякий товар либо служба владеют собственными особенностями.

Значимые нюансы при построении многоугольника конкурентоспособности

Позже построения осей и определения их значения с поддержкой системы баллов определяется место имеющихся товаров либо предприятий на них. Для создания многоугольника следует опрятно объединить точки – показатели. Оценив полученные фигуры, дозволено сделать итог об имеющихся превосходствах и недостатках оцениваемых объектов. После этого происходит энергичное закрепление позитивных сторон и начинается энергичная работа по ликвидации упущений, найденных в ходе сравнительного обзора.