Совет 1: Как обнаружить нормаль плоскости
Нормаль плоскости n (вектор нормали к плоскости) – это всякий направленный перпендикуляр к ней (ортогональный вектор). Последующие выкладки по определении нормали зависят от метода задания плоскости.
Инструкция
1. Если задано всеобщее уравнение плоскости – AX+BY+CZ+D=0 либо его форма A(x-x0)+B(y-y0)+C(z-z0)=0, то дозволено сразу записать результат – n(А, В, С). Дело в том, что это уравнение было получено, как задача определения уравнения плоскости по нормали и точке.
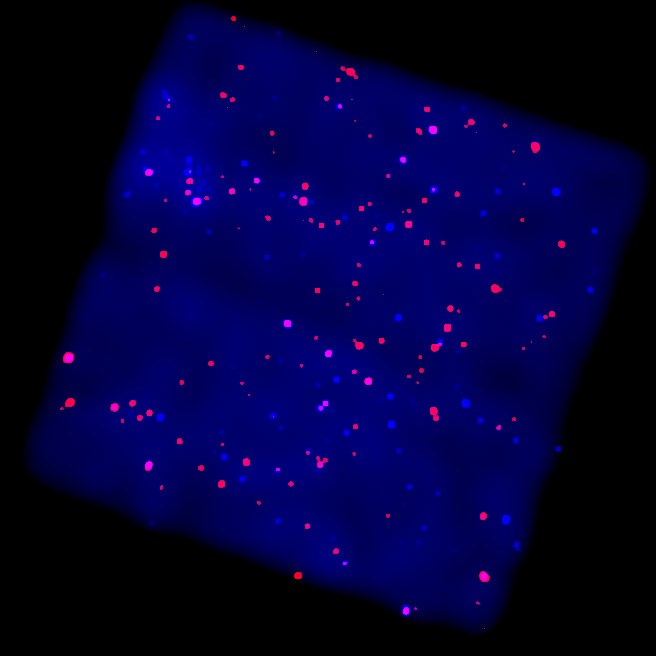
2. Для приобретения всеобщего результата, вам потребуется векторное произведение векторов из-за того, что последнее неизменно перпендикулярно начальным векторам. Выходит, векторным произведением векторов, является определенный вектор, модуль которого равен произведению модуля первого (а) на модуль второго (b) и на синус угла между ними. При этом данный вектор (обозначьте его через n) ортогонален a и b – это основное. Тройка этих векторов правая, то есть из конца n кратчайший поворот от a к b совершается вопреки часовой стрелки. [a,b] – одно из общепризнанных обозначений векторного произведения. Для вычисления векторного произведения в координатной форме, применяется вектор-определитель (см. рис.1)
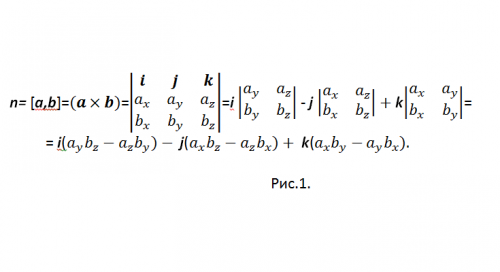
3. Для того дабы не путаться со знаком «-», перепишите итог в виде: n={nx, ny, nz}=i(aybz-azby)+j(azbx-axbz)+k(axby-aybx), и в координатах: {nx, ny, nz}={(aybz-azby), (azbx-axbz), (axby-aybx)}.Больше того, чтобы не путаться с численными примерами выпишете все полученные значения по отдельности: nx=aybz-azby, ny=azbx-axbz, nz=axby-aybx.
4. Вернитесь к решению поставленной задачи. Плоскость дозволено задать разными методами. Пускай нормаль к плоскости определяется двумя неколлинеарными векторами, причем сразу численно. Пускай даны векторы a(2, 4, 5) и b(3, 2, 6). Нормаль к плоскости совпадает с их векторным произведением и, как только что было выяснено будет равна n(nx, ny, nz),nx=aybz-azby, ny=azbx-axbz, nz=axby-aybx. В данном случае ax=2, ay=4, az=5, bx=3, by=2, bz=6. Таким образом, nx=24-10=14, ny=12-15=-3, nz=4-8=-4. Нормаль обнаружена – n(14, -3, -4). При этом она является нормалью к целому семейству плоскостей.
Совет 2: Как обнаружить нормаль
Под математическим термином нормаль прячется больше привычное на слух представление перпендикуляра. То есть задача нахождения нормали подразумевает поиск уравнения прямой, перпендикулярной к заданной косой либо поверхности, проходящей через определенную точку. В зависимости от того, на плоскости либо в пространстве требуется обнаружить нормаль , данная задача решается по-различному. Разглядим оба варианта задачи.
Вам понадобится
- умение находить производные функции, знание находить частные производные функции нескольких переменных
Инструкция
1. Нормаль к косой, заданной на плоскости в виде уравнения у = f(x).Находим значение функции, которая определяет уравнение данной косой в точке, в которой ищется уравнение нормали: а = f(x0). Находим производную к данной функции: f'(x). Ищем значение производной в этой же точке: B = f'(x0). Вычисляем значение дальнейшего выражения: C = a – B*x0. Составляем уравнение нормали, которое будет иметь вид: у = B*x + C.
2. Нормаль к поверхности либо косой, заданной в пространстве в виде уравнения f = f(x,y,z).Находим частные производные к данной нам функции: f’x(x,y,z), f’y(x,y,z), f’z(x,y,z). Ищем значение этих производных в точке М(x0,y0,z0) – точка, в которой нужно обнаружить уравнение нормали к поверхности либо пространственной косой: A = f’x(x0,y0,z0), B = f’y(x0,y0,z0), C = f’z(x0,y0,z0). Составляем уравнение нормали, которое будет иметь вид: (x – x0)/A = (y – y0)/B = (z – z0)/C
3. Пример:Обнаружим уравнение нормали к функции у = х – х^2 в точке х = 1.Значение функции в данной точке а = 1 – 1 = 0.Производная к функции у’ = 1 – 2х, в данной точке В = у'(1) = -1.Вычисляем С = 0 – (-1)*1 = 1.Желанное уравнение нормали имеет вид: у = -х + 1
Видео по теме
Полезный совет
Частные производные всякий функции нетрудно обнаружить, представив, что все переменные, помимо той которая является исследуемой – константы.
Совет 3: Как обнаружить вектор нормали
Задача поиска вектора нормали прямой на плоскости и плоскости в пространстве слишком примитивна. Реально она завершается записью всеобщих уравнений прямой либо плоскости. От того что кривая на плоскости каждого лишь частный случай поверхности в пространстве, то именно о нормалях к поверхности и пойдет речь.
Инструкция
1. 1-й метод Данный метод самый примитивный, но для его понимания требуется умение представления скалярного поля. Однако, и неискушенный в этом вопросе читатель сумеет применять результирующие формулы данного вопроса.
2. Знаменито, что скалярное поле f задается как f=f(x, y, z), а любая поверхность при этом – это поверхность яруса f(x, y, z)=C (C=const). Помимо того, нормаль поверхности яруса совпадает с градиентом скалярного поля в заданной точке.
3. Градиентом скалярно поля (функции 3 переменных) именуется вектор g=gradf=iдf/дx+jдf/дy+kдf/дz={дf/дx, дf/дy, дf/дz}. Потому что длина нормали значения не имеет, остается лишь записать результат. Нормаль к поверхностиf(x, y, z)-C=0 в точкеM0(x0, y0, z0) n=gradf=iдf/дx+jдf/дy+kдf/дz={дf/дx, дf/дy, дf/дz}.
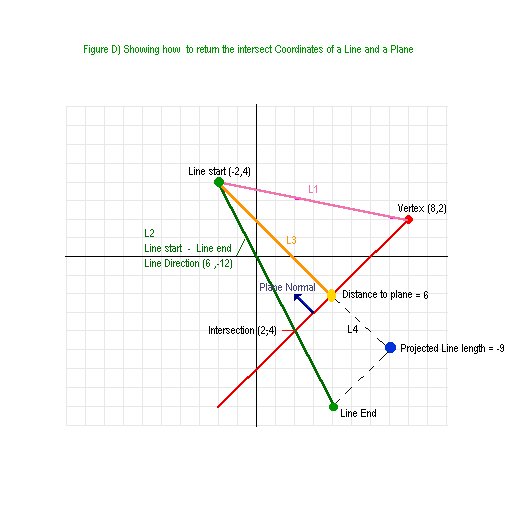
4. 2-й метод Пускай поверхность задана уравнением F(x, y, z)=0. Дабы дозволено было в будущем провести аналогии с первым методом, следует рассматривать, что производная непрерывной равна нулю, и F задается как f(x, y, z)-C=0 (C=const). Если провести сечение этой поверхности произвольной плоскостью, то возникшую пространственную кривую дозволено считать годографом какой-нибудь вектор-функции r(t)= ix(t)x+jy(t)+kz(t). Тогда производная вектора r’(t)= ix’(t)+jy’(t)+kz’(t) направлена по касательной в некоторой точке M0(x0, y0, z0) поверхности (см. рис.1).
5. Чтобы не появилось путаницы, нынешние координаты касательной прямой следует обозначить, скажем, курсивом (x, y, z). Канонические уравнение касательной прямой, с учетом, что r’(t0) – направляющий вектор, записывается как (x-x(t0))/(dx(t0)/dt)= (y-y(t0))/(dy(t0)/dt)= (z-z(t0))/(dz(t0)/dt).
6. Подставив координаты вектор-функции в уравнение поверхности f(x, y, z)-C=0 и продифференцировав по t вы получите (дf/дx)(дx/дt)+(дf/дy) (дy/дt)+(дf/дz)(дz/дt)=0. Равенство представляет собой скалярное произведение некоторого вектора n(дf/дx, дf/дy, дf/дz) и r’(x’(t), y’(t), z’(t)). Потому что оно равно нулю, то n(дf/дx, дf/дy, дf/дz) и есть желанный вектор нормали . Видимо, что итоги обоих методов одинаковы.
7. Пример (имеет теоретическое значение). Обнаружить вектор нормали к поверхности заданной типичным уравнением функции 2-х переменных z=z(x, y). Решение. Перепишите это уравнение в форме z-z(x, y)=F(x, y, z)=0. Следуя любому из предложных методов, получается, что n(-дz/дx, -дz/дy, 1) – желанный вектор нормали .








