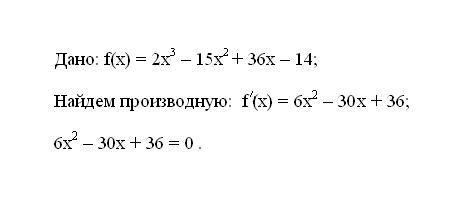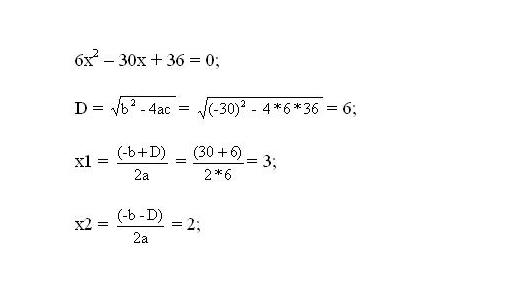Совет 1: Как обнаружить экстремум
Экстремумы представляют собой максимальные и минимальные значения функции и относятся к ее главнейшим колляциям. Экстремумы находятся в скептических точках функций. Причем функция в экстремуме минимума и максимума меняет свое направление соответственно знаку. Согласно определению, первая производная от функции в точке экстремума равна нулю либо отсутствует. Таким образом, поиск экстремумов функции складывается из 2-х задач: нахождения производной для заданной функции и определения корней ее уравнения.
Инструкция
1. Запишите заданную функцию f(x). Определите ее первую производную f’(x). Полученное выражение производной приравняйте к нулю.
2. Решите полученное уравнение. Корни уравнения будут являться скептическими точками функции.
3. Определите, какими скептическими точками – минимума либо максимума – являются полученные корни. Для этого обнаружьте вторую производную f’’(x) от начальной функции. Подставьте в нее по очереди значения скептических точек и высчитайте выражение. Если вторая производная от функции в скептической точке огромнее нуля, то это будет точка минимума. Напротив – точка максимума.
4. Посчитайте значение начальной функции в полученных точках минимума и максимума. Для этого подставьте их значения в выражение функции и вычислите. Полученное число будет определять экстремум функции. Причем, если скептическая точка была максимумом, экстремум функции также будет максимумом. Также в минимальной скептической точке функция будет добиваться свой наименьший экстремум.
Совет 2: Как обнаружить экстремум функции 2-х переменных
По определению, точка М0(x0, y0) именуется точкой локального максимума (минимума) функции 2-х переменных z=f(x,y), если в некоторой окрестности точки U(x0, y0), для всякий точки M(x, y) исполнено f(x,y)f(x0, y0)). Эти точки именуются экстремумами функции . В тексте частные производные обозначаются в соответствии с рис. 1.

Инструкция
1. Нужным условием экстремума является равенство нулю частных производных функции по x и по y. Точка M0(x0, y0), в которой в нуль обращаются обе частные производные, именуется стационарной точкой функции z=f(x, y).
2. Примечание. Частные производные функции z=f(x, y) могут не существовать в точке экстремума, следственно точками допустимого экстремума являются не только стационарные точки, но и точки, в которых частные производные не существуют (им соответствуют острия поверхности – графика функции ).
3. Сейчас дозволено перейти к довольным условиям наличия экстремума. Если дифференцируемая функция имеет экстремум, то он может быть только в стационарной точке. Довольные данные экстремума формулируются дальнейшим образом: пускай в некоторой окрестности стационарной точки (x0, y0) функция f(x, y) имеет постоянные частные производные второго порядка. Скажем: (cм. рис.2)
4. Тогда: а) если Q>0, то в точке (x0, y0) функция имеет экстремум, причем при f’’(x0, y0)0) – локальный минимум; б) если Q
5. Для отыскания экстремума функции 2-х переменных дозволено предложить следующую схему: вначале находятся стационарные точки функции . После этого в этих точках проверяются довольные данные экстремума. Если функция в каких-то точках не имеет частных производных, то в этих точках тоже может быть экстремум, но довольные данные теснее не будут применимы.
6. Пример. Обнаружить экстремумы функции z=x^3+y^3-xy.Решение. Обнаружим стационарные точки функции (см. рис. 3):
7. Решение последней системы дает стационарные точки (0, 0) и (1/3, 1/3). Сейчас нужно проверить выполнение довольного данные экстремума. Обнаружьте вторые производные, а также стационарные точки Q(0,0 ) и Q(1/3, 1/3) (см. рис 4):
8. Потому что Q(0, 0)0, следственно, в точке (1/3, 1/3) экстремум есть. С учетом того, что вторая производная (по xx) в (1/3, 1/3) огромнее нуля, нужно принять решение, что эта точка является минимумом.
Совет 3: Как обнаружить наибольшее наименьшее значение функции
Феноменальный немецкий математик Карл Вейерштрасс подтвердил, что для всякой постоянной на отрезке функции существуют ее наибольшее и наименьшее значение на этом отрезке. Задача определения наибольшего и наименьшего значения функции имеет широкое прикладное значение в экономике, математике, физике и других науках.
Вам понадобится
- чистый лист бумаги;
- ручка либо карандаш;
- учебник по высшей математике.
Инструкция
1. Пускай функция f(x) постоянна и определена на заданном отрезке [a; b] и имеет на нем некоторое (финальное) число скептических точек. Первым делом обнаружим производную функции f'(x) по х.
2. Приравниваем производную функции к нулю, дабы определить скептические точки функции. Не забываем определить точки, в которых производная не существует – они также являются скептическими.
3. Из множества обнаруженных скептических точек выбираем те, которые принадлежат отрезку [a; b]. Вычисляем значения функции f(x) в этих точках и на концах отрезка.
4. Из множества обнаруженных значений функции выбираем наивысшее и минимальное значения. Это и есть желанные наибольшее и наименьшее значения функции на отрезке.
Видео по теме
Совет 4: Как обнаружить интервалы монотонности и экстремума
Изыскание поведения функции, имеющей трудную связанность от довода, проводится с поддержкой производной. По нраву метаморфозы производной дозволено обнаружить скептические точки и участки роста либо убывания функции.

Инструкция
1. На разных участках числовой плоскости функция ведет себя по-различному. При пересечении оси ординат функция меняет знак, проходя нулевое значение. Однообразный подъем может сменяться убыванием при прохождении функции через скептические точки — экстремумы. Обнаружить экстремумы функции, точки пересечения с координатными осями, участки однообразного поведения — все эти задачи решаются при обзоре поведения производной.
2. Перед началом изыскания поведения функции Y = F(x) оцените область возможных значений довода. Принимайте к рассмотрению только те значения самостоятельной переменной «х», при которой допустимо существование функции Y.
3. Проверьте, является ли заданная функция дифференцируемой на рассматриваемом промежутке числовой оси. Обнаружьте первую производную заданной функции Y’ = F'(x). Если F'(x)>0 для всех значений довода, то функция Y = F(x) на этом отрезке нарастает. Правильно и обратное заявление: если на промежутке F'(x)